Тема 9. Корреляционно-регрессионный анализ

Корреляционно-регрессионный анализ заключается в определении аналитического выражения и степени тесноты связи между различными социально-экономическими явлениями и процессами или их признаками.

Признаки, обусловливающие изменение других, связанных с ними признаков, называют факторными и обозначают х. Признаки, изменяющиеся под воздействием факторных признаков, называют результативными и обозначают .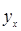

Связи между явлениями и их признаками классифицируются по:

– аналитическому выражению (линейная связь и нелинейная связь);

– направлению (прямая связь и обратная связь);

– степени тесноты (связь отсутствует, слабая, умеренная, сильная).

Линейная связь выражается уравнением прямой

,

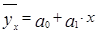где 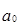и 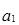– параметры линейной функции в уравнении связи, выражающей зависимость у от х.

Степень тесноты связи между различными явлениями определяют с помощью эмпирического корреляционного отношения () ,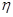

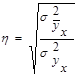где 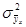– дисперсия в ряду результативного признака под влиянием фактора х, т. е. рассчитанных по уравнению регрессии;

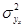– дисперсия в ряду фактических значений результативного признака.

Если 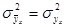, т. е. 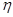= 1, то существует полная зависимость у_x от х. Если 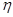= 0, то вариация факторного признака не влияет на вариацию результативного признака.

В случае линейной зависимости между двумя признаками степень тесноты связи между ними можно определить также с помощью линейного коэффициента корреляции по формулам

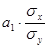r = и r = ,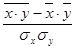

где 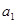– параметр линейной функции в уравнении связи, выражающей зависимость у от х;

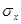и 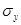– среднеквадратическое отклонение в рядах х и у, соответственно;

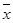– средняя величина факторного признака;

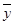– средняя величина результативного признака;

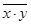– средняя величина произведений факторного и результативного признаков.

Коэффициент регрессии 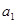показывает, на сколько единиц изменяются значения результативного признака при изменении факторного признака на единицу. В случае прямой связи между признаками линейный коэффициент корреляции принимает положительные значения, а в случае обратной связи – отрицательные.

По величине линейного коэффициента корреляции судят о степени тесноты связи между признаками.

Величина коэффициента корреляции по модулю	Теснота связи
От 0 до ± 0,3	практически отсутствует
От ± 0,3 до ± 0,5	слабая
От ± 0,5 до ± 0,7	умеренная
От ± 0,7 до ± 1,0	сильная

Графически связь между двумя количественными признаками изучают с помощью поля корреляции.

Пример 1. Приводятся данные за 2004 г. по отдельным отраслям промышленности в целом по РФ:

Отрасль промышленности	Среднегодовая численность персонала, тыс. чел.	Объем промышленной продукции, млрд. руб.	Среднемесячная номинальная заработная плата, тыс. руб.
Электроэнергетика			10,96
Топливная		1 996	19,35
Черная металлургия		1 126	9,35
Цветная металлургия			13,45
Машиностроение	3 180	1 748	6,68

Составить уравнение линейной функции, выражающей зависимость среднемесячной заработной платы от уровня производительности труда, и измерить тесноту связи между этими показателями. Полученную связь изучить графически.

Решение. Все предварительные расчеты представим в таблице. Факторный признак – уровень производительности труда, рассчитанная путем деления объема промышленной продукции на среднегодовую численность персонала (графа 2), результативный признак – размер средней месячной номинальной заработной платы (графа 3).

Отрасль промышлен-ности	x	y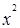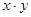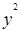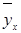
Электро-энергетика	1,127	10,96	1,2701	12,3519	120,1216	10,405
Топливная	2,630	19,35	6,9169	50,8906	374,4225	18,402
Черная металлургия	1,632	9,35	2,6634	15,2592	87,4225	13,092
Цветная металлургия	1,155	13,45	1,3340	15,5348	180,9025	10,554
Машино-строение	0,550	6,68	0,3025	3,6740	44,6224	7,336
Итого	7,094	59,79	12,4869	97,7159	807,4915	59,789

Вычисляем все необходимые показатели.

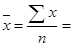
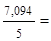1,4188;

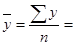
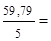11,958;

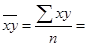
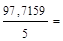19,54318;

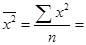
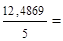2,49738;

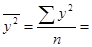
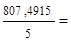61,64983;

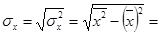
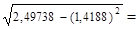0,696;

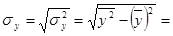
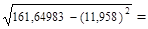4,319.

Вычислим линейный коэффициент корреляции

r = 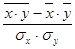= = 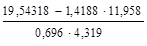0,857.

Для определения параметров линейной функци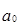и и 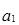составляют систему уравнений

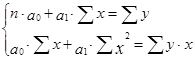
Подставим в систему уравнений все вычисленные показатели

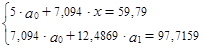
Решая эту систему уравнений, получаем, что 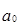= 4,40930 и 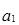= 5,32048.

Уравнение имеет вид: .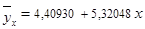

В графе 7 с помощью полученной линейной функции рассчитаем теоретические значения результативного признака.

Вычислим линейный коэффициент корреляции

r = 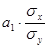= = 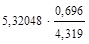0,857.

Зависимость средней месячной номинальной заработной платы от уровня производительности труда в представленных отраслях промышленности сильная (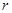 близок к 1) и прямая ( 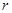больше нуля), т. е. с увеличением производительности труда увеличивается среднемесячная номинальная заработная плата. Построим поле корреляции.

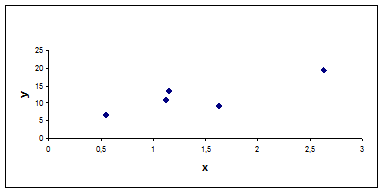
Рис. 8. Поле корреляции

Поскольку наблюдается сосредоточение точек на графике, то существует сильная связь между уровнем производительности труда и среднемесячной номинальной заработной платой.

Оценку существенности корреляционной связи производят с помощью F -критерия Фишера и t -критерия Стьюдента.

Коэффициент эластичности ( 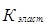) показывает, на сколько процентов изменяется результативный признак при изменении факторного признака на 1% и рассчитывается по формуле = ,

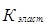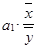где 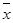– среднее значение факторного признака;

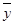– среднее значение результативного признака;

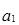– параметр линейной функции, выражающей зависимость у от х.

Если с возрастанием факторного признака происходит ускоренное возрастание или убывание результативного признака, то корреляционная зависимость может быть выражена параболой второго порядка

.

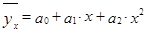Система уравнений для расчета параметров параболы второго порядка принимает вид

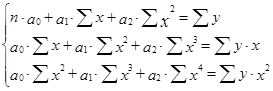
При наличии линейной зависимости результативного признака от двух факторных признаков вычисляют множественный коэффициент корреляции

R = ,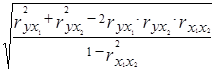

где r – парные коэффициенты корреляции между признаками.

Множественный коэффициент корреляции изменяется в пределах от 0 до + 1, и его приближение к единице свидетельствует о сильной зависимости между рассматриваемыми признаками.