Ранговые коэффициенты связи

Коэффициент корреляции рангов Спирмена (r) определяется по формуле

r = ,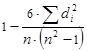

где 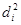– квадраты разности рангов;

n – число наблюдений (число пар рангов).

Коэффициент корреляции рангов Кендалла (t) вычисляют по формуле

t = ,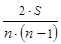

где S – сумма разностей между числом последовательностей и числом инверсий по результативному признаку,

n – число наблюдений (пар рангов).

Коэффициенты Спирмена и Кендалла принимают значения от –1 до + 1. Чем ближе величина коэффициентов Спирмена и Кендалла по модулю к 1, тем сильнее связь между признаками.

Пример 2. По исходным данным предыдущего примера 1 рассчитать ранговые коэффициенты связи Спирмена и Кендалла.

Решение. Ранжируем значения факторного и результативного признаков (графы 4 и 5); находим разности рангов 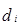= 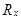– 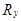(графа 6).

Отрасль промышленности	х	у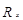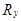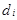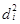
Электроэнергетика	1,127	10,96			–1
Топливная	2,630	19,35
Черная металлургия	1,632	9,35
Цветная металлургия	1,155	13,45			–1
Машиностроение	0,550	6,68
Итого	–	–	–	–	–

Полученные разности рангов (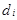) возводим в квадрат, находим их сумму (графа 7) и подставляем в формулу коэффициента Спирмена

r = 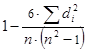= = 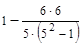= 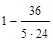0,7.

При вычислении коэффициента Кендалла значения факторного признакапредварительно ранжируем. Значения результативного признака записываем в соответствии с исходными данными.

Отрасль промышленности	х	у		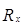	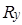P	Q
Машиностроение	0,550	6,68
Электроэнергетика	1,127	10,96
Цветная металлургия	1,155	13,45
Черная металлургия	1,632	9,35
Топливная	2,630	19,35
Итого						– 2

Для каждого 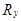определяем:

– число следующих за ним рангов, больших по значению, чем данный ранг. Общее число таких случаев учитывают со знаком «+» и обозначают буквой P (графа 6);

– число следующих за ним рангов, меньших по значению, чем данный ранг. Общее число таких случаев учитывают со знаком «–» и обозначают буквой Q (графа 7).

Вычисляем S = P + Q = 8 + (–2) = 6.

Подставим в формулу коэффициента Кендалла полученные значения

t = 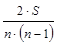= = 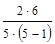0,6.

Величины коэффициентов Спирмена и Кендалла свидетельствует о тесной зависимости среднемесячной заработной платы от уровня производительности труда в представленных отраслях экономики.

Для изучения степени тесноты связи между произвольным числом ранжированных количественных признаков вычисляют множественный коэффициент конкордации (W) по формуле

,

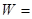
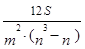где S – отклонение суммы квадратов рангов от средней квадратов рангов;

m – число ранжируемых признаков;

n – число наблюдений.

Эта формула применяется в том случае, когда ранги по каждому признаку не повторяются.

Если несколько значений имеют одинаковую количественную оценку, т. е. ранги повторяются, то применяют следующую формулу:

,

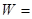
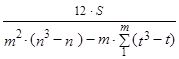где t – число одинаковых рангов по каждому признаку.