Комбинаторика событий

изучает способы подсчёта числа событий.

Тип события	Число всевозможных наборов N	Замечания
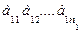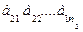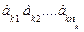
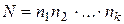
Упорядоченный набор по одному элементу из различных групп 1 гр: 2 гр: … k гр:		Если 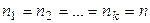, то
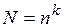
Упорядоченный набор k элементов из совокупности 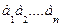с возвращением
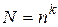
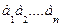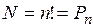
Упорядоченный набор всех элементов из совокупности без возвращения		Перестановками называют наборы, составленные из одних и тех же n различных элементов и отличающиеся только порядком расположения элементов.
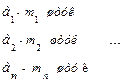
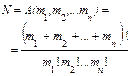
Упорядоченный набор всех элементов из совокупности без возвращения, если исходная совокупность состоит из повторяющихся элементов		Строки (наборы) заданного состава, отличающиеся порядком расположения элементов, называются перестановками с повторениями
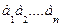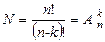
Упорядоченный набор k элементов из совокупности без возвращения		Размещениями называют наборы из k элементов, составленные из совокупности, содержащей n различных элементов, которые отличаются либо составом элементов, либо их порядком.
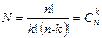
Произвольный набор k элементов из совокупности без возвращения		Сочетаниями называют наборы, составленные из n различных элементов по k элементов, которые отличаются только составом элементов.
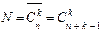
Произвольный набор k элементов из различных n совокупностей без возвращения		Различные составы строк (наборов) заданной длины (размера) k, составленные из элементов n -ого числа множеств, называются сочетаниями с повторениями

Замечания:

1. ,

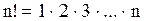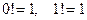
2. 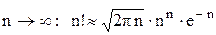– формула Стирлинга

3.

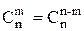
4.

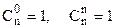
При решении задач комбинаторики используют правила:

· Правило суммы – если некоторый объект А может быть выбран из множества объектов N способами, а объект В может быть выбран M способами, то выбрать объект А или В можно (N+M) способами.

· Правило произведения – если некоторый объект А может быть выбран из множества объектов N способами, и после каждого такого выбора объект В может быть выбран M способами, то выбрать пару объектов (А; В) можно (N·M) способами.