Теорема умножения 1 (для зависимых событий):
Если события 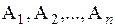 – зависимы, то вероятность их одновременного наступления (произведения) вычисляется по формуле
– зависимы, то вероятность их одновременного наступления (произведения) вычисляется по формуле
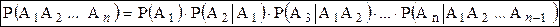 ,
,
где 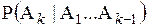 условная вероятность события
условная вероятность события 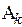 , вычисленная в предположении, что все предшествующие события имели место.
, вычисленная в предположении, что все предшествующие события имели место.
► 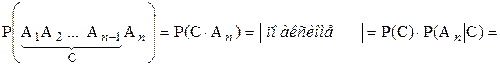
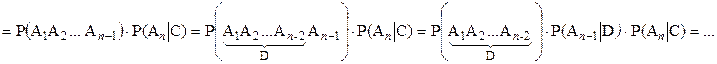
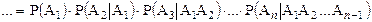 ■
■
Теорема умножения 2 (для независимых событий):
Если события 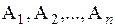 – независимы, то вероятность их одновременного наступления (произведения) вычисляется по формуле:
– независимы, то вероятность их одновременного наступления (произведения) вычисляется по формуле: 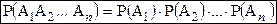
► На основании теоремы 1 и факта, что для независимых событий А и В справедливо равенство 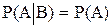 . ■
. ■
Теорема сложения 1 (для несовместных событий):
Если события 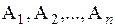 – несовместны, то вероятность наступления одного из них (суммы) вычисляется по формуле:
– несовместны, то вероятность наступления одного из них (суммы) вычисляется по формуле: 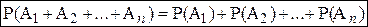 .
.
► 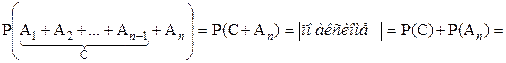
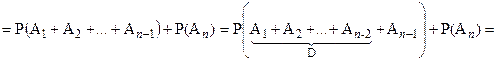
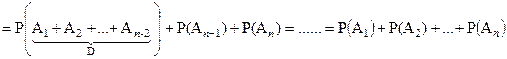 ■
■
Теорема сложения 2 (для совместных событий):
Если события 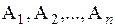 – совместны, то вероятность наступления хотя бы одного из них (суммы) вычисляется по формуле:
– совместны, то вероятность наступления хотя бы одного из них (суммы) вычисляется по формуле: 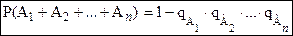 ,
,
где 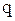 – вероятность не наступления события.
– вероятность не наступления события.
► Событие С– «произойдёт хотя бы одно из двух совместных событий А и В», т. е. 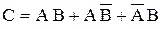 . Тогда полную группу событий
. Тогда полную группу событий 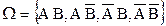 можно представить в виде
можно представить в виде 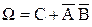 , где события
, где события 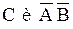 – несовместны.
– несовместны.
По теореме сложения 1 и теореме умножения 2: 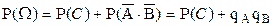 .
.
Учитывая, что 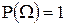 , окончательно получим
, окончательно получим 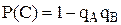 . ■
. ■
Замечание: Если вероятность наступления события А в каждом из n испытаний равна p, то вероятность наступления события А в n испытаниях: 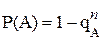 .
.
Теорема (наступление только одного из двух совместных событий):
Если события 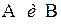 – совместны, то вероятность наступления только одного из них вычисляется по формуле:
– совместны, то вероятность наступления только одного из них вычисляется по формуле: 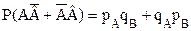
где p –вероятность наступления события, q – вероятность не наступления события.
► Событие С – «произойдёт только одно из двух совместных событий А или В»,
т. е. 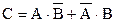 , где
, где 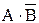 и
и 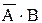 - несовместные события.
- несовместные события.
Тогда по теореме 1: 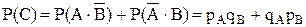 . ■
. ■
 2015-03-20
2015-03-20 347
347








