1. Составим бином Ньютона для p и q:
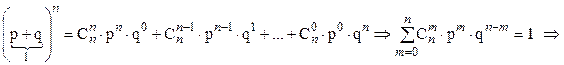
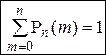
2. Вероятность наступления события А в интервале [ m 1, m 2] раз при п испытаниях определяется по формуле: 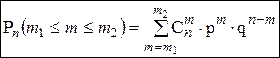
II. При больших значениях n (n→∞) применение формулы Бернулли приводит к большим вычислениям. Поэтому используют приближённые формулы.
A) При n→∞ и малых вероятностях p(p<<0,1).
Обозначим 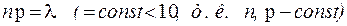 . Откуда
. Откуда 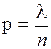 .
.
Тогда формула Бернулли примет вид:
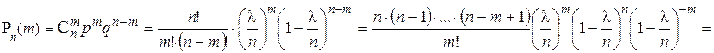
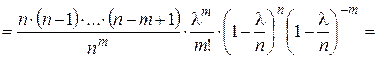
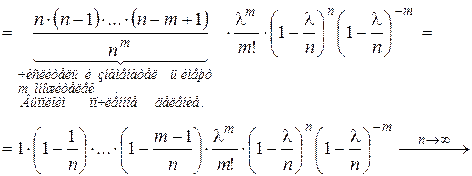
Учитывая, что 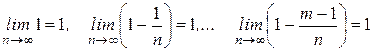 ,
, 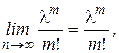
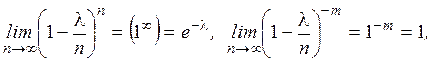
получим: 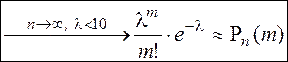 – формула Пуассона
– формула Пуассона
B) При больших значениях n (n→∞) и не малых вероятностях p формула Пуассона даёт погрешность. В связи с этим применяется другое приближение, использующее предельный переход и формулу Стирлинга, – локальная формула Муавра-Лапласа:
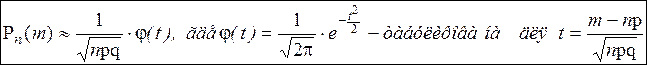
Замечание. Так как вероятность наступления события А в интервале [ m 1, m 2] раз при п испытаниях определяется по формуле: 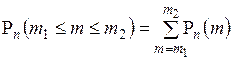 , то с учётом предельного перехода, имеем интегральную формулу Муавра-Лапласа:
, то с учётом предельного перехода, имеем интегральную формулу Муавра-Лапласа:
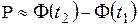 ,
где ,
где 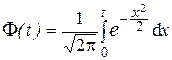 – табулирована для – табулирована для 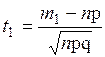 , , 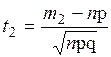
|
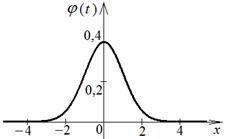
Свойства функции Гаусса 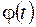
| Свойства функции Лапласа 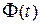
|
1. Чётность: 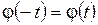 2. Для
2. Для 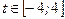 : : 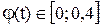 3. Для
3. Для 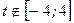 : : 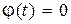 4.
4. 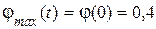
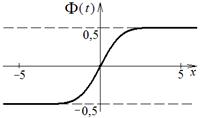
| 1. Нечётность 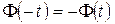 2. Для
2. Для 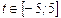 : : 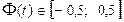 3. Для
3. Для 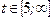 : : 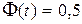
|
 2015-03-20
2015-03-20 451
451








