Рядом распределения дискретной СВ 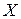 называется упорядоченный ряд различных значений СВ (в порядке возрастания или убывания) и соответствующих им вероятностей:
называется упорядоченный ряд различных значений СВ (в порядке возрастания или убывания) и соответствующих им вероятностей:
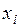 | 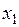 | 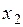 | … | 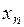 | … | 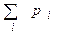 |
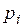 | 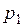 | 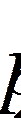 | 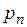 |
Простейшим примером ДСВ является индикатор события А: 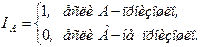
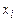 | ||
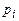 | 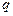 | 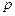 |
Для него ряд распределения имеет вид: где 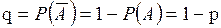 . . | 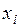 | ||
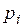 | p | q |
Ряд распределения можно проиллюстрировать на графике:
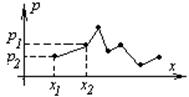 | Многоугольником распределения называется ломаная, соединяющая точки 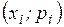 . . |
Граф также может изображать распределение. Где 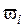 – элементарные события, – элементарные события, 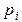 –соответствующие вероятности –соответствующие вероятности | 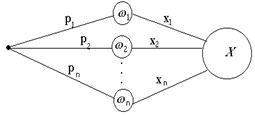 |
· Над СВ X можно производить различные функциональные операции. Закон распределения при этом не изменяется.
| Если СВ X имеет ряд распределения: | 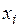 | 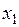 | … | 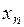 | … | 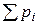 |
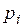 | 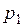 | 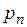 | ||||
то ряд распределения новой СВ 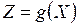 имеет вид: имеет вид: | ||||||
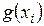 | 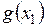 | … | 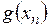 | … | 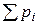 | |
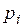 | 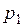 | 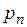 |
· При выполнении функциональных операций над совокупностью СВ X и Y, имеющих соответствующие таблицы распределения, применяют правило:
Вероятность события 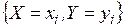 , означающего одновременное появление событий
, означающего одновременное появление событий 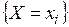 и
и 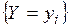 , равна произведению соответствующих вероятностей:
, равна произведению соответствующих вероятностей:
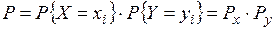
II. Интегральный закон распределения
Интегральной функцией распределения дискретной СВ 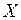 называется функция
называется функция 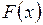 , которая для любого действительного числа
, которая для любого действительного числа 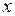 равна вероятности события
равна вероятности события 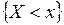 :
:
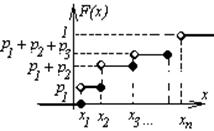
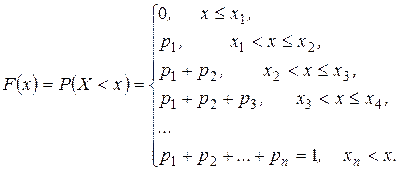
Теорема: Вероятность попадания значений СВ в интервал 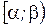 определяется формулой:
определяется формулой: 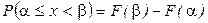 .
.
► Рассмотрим события
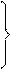
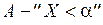 ;
;
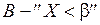 ; тогда
; тогда 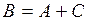
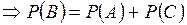 ,
,
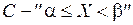 т.е.
т.е. 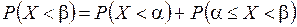
но 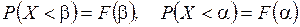 .
.
Следовательно, 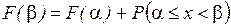 . ■
. ■
Свойства интегральной функции:
1. 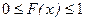 ,т.к.
,т.к. 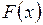 – есть вероятность по определению.
– есть вероятность по определению.
2. 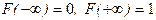 – по определению.
– по определению.
3. 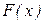 – неубывающая функция.
– неубывающая функция.
►Определим 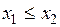 . Тогда:
. Тогда: 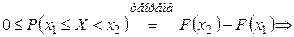
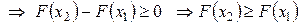 ■
■
 2015-03-20
2015-03-20 1161
1161
