I. Интегральный закон распределения
Интегральной функцией распределения непрерывной СВ 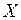 называется функция
называется функция 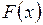 , которая для любого действительного числа
, которая для любого действительного числа 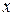 равна вероятности события
равна вероятности события 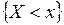 :
:
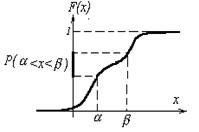
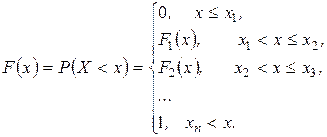
Теорема: Вероятность попадания значений СВ в интервал 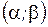 определяется формулой:
определяется формулой: 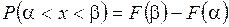 .
.
Замечание: Для непрерывной СВ вероятность попасть в точку равна нулю, поэтому интервал 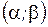 может быть закрытым или полуоткрытым.
может быть закрытым или полуоткрытым.
| Свойства интегральной функции: | 1. 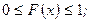 2. 2. 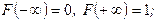 3. 3. 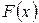 –неубывающая функция; 4. –неубывающая функция; 4. 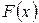 – непрерывная функция. – непрерывная функция. |
II. Дифференциальный закон распределения
Дифференциальной функцией распределения непрерывной СВ 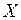 (плотностью распределения) называется функция:
(плотностью распределения) называется функция: 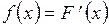 ,
,
где 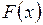 – интегральная функция распределения СВ.
– интегральная функция распределения СВ.
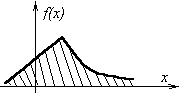
Плотность распределения указывает на то, как часто СВ появляется в некоторой окрестности т. x при повторении опытов.
График плотности распределения  называется кривой распределения.
называется кривой распределения.
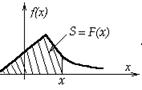 Теорема:
Теорема: 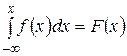 .
.
► У читывая определение, по формуле Ньютона–Лейбница имеем
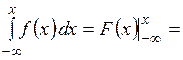
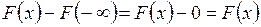 . ■
. ■
Теорема: 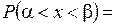
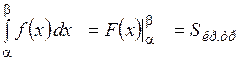 .
.
► 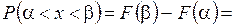
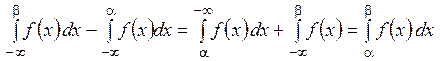 . ■
. ■
Свойства плотности распределения:
1. 
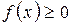 .
.
►Т.к. 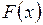 –неубывающая функция, то
–неубывающая функция, то 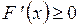 . ■
. ■
2. 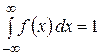 .
.
– это означает, что площадь соответствующей криволинейной трапеции =1.
► 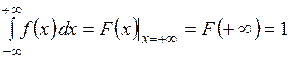 . ■
. ■
 2015-03-20
2015-03-20 827
827








