Числовые характеристики СВ– это числа, которые характеризуют особенности распределения СВ.
I. Модой СВ X (обозн: 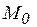 ) называется такое значение СВ:
) называется такое значение СВ:
| в случае дискретной СВ | в случае непрерывной СВ | |
| которому соответствует максимальное значение вероятности. | которому соответствует максимум дифференциальной функции. | |
| · Если график распределения СВ X обладает единственным локальным максимумом, то распределение называется модальным. | 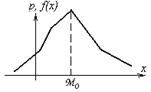 | |
| · Если график распределения имеет несколько локальных максимумов, то распределение называется полимодальным. | 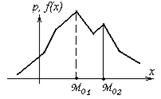 | |
| · Если график распределения не имеет локальных максимумов, но имеет локальный минимум, то распределение называется антимодальным | 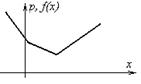 | |
II. Медианой СВ X называется значение СВ (обозн: 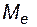 ), для которого справедливо:
), для которого справедливо:
| в случае дискретной СВ | в случае непрерывной СВ |
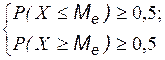 | 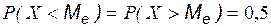 Графически – это точка Графически – это точка 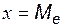 , для которой прямая , для которой прямая 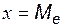 делит пополам площадь криволинейной трапеции, ограниченной кривой распределения. делит пополам площадь криволинейной трапеции, ограниченной кривой распределения. |
III. Математическим ожиданием СВ называется ориентировочное (среднее) число, около которого группируются все возможные значения СВ. (Обозн: 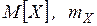 )
)
1) Если 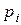 принять за "вес" значения
принять за "вес" значения 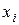 дискретной СВ, то центр масс
дискретной СВ, то центр масс 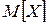 будет определяться формулой:
будет определяться формулой: 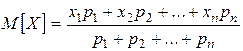 ,
,
учитывая что 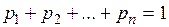 , получим:
, получим: 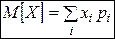
2) В случае с непрерывной СВ точечная вероятность 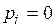 . Поэтому работают с интервальной вероятностью:
. Поэтому работают с интервальной вероятностью: 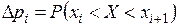 , которая равна площади частичной криволинейной трапеции графика дифференциальной функции СВ.
, которая равна площади частичной криволинейной трапеции графика дифференциальной функции СВ.
При большом разбиении интервала значений СВ 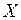 частичная криволинейная трапеция принимает форму прямоугольника, следовательно
частичная криволинейная трапеция принимает форму прямоугольника, следовательно 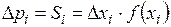 .
.
Тогда 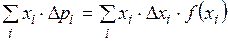 . Переходя к пределу, получим:
. Переходя к пределу, получим:
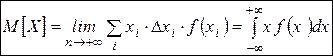
Замечания:
1. Если над СВ 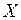 выполняют функциональные операции и получают новую СВ
выполняют функциональные операции и получают новую СВ 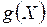 , то
, то 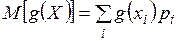 , где
, где 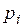 – вероятности значений
– вероятности значений 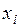 .
.
2. Математическое ожидание существует не для всех СВ.
¨ Если распределение является: – симметричным;
– модальным;
и для него существует математическое ожидание,
то оно (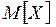 ) совпадает с медианой
) совпадает с медианой 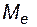 и модой
и модой 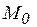 – центром симметрии распределения.
– центром симметрии распределения.
Свойства:
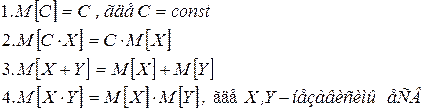
Следствие: 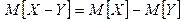
Доказательства свойств 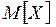 для дискретной СВ:
для дискретной СВ:
1. 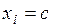 . Т.е. с – единственно возможноезначение СВ, т.е. оно достоверно.
. Т.е. с – единственно возможноезначение СВ, т.е. оно достоверно.
Тогда 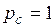 . В результате
. В результате 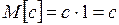 ■
■
2. 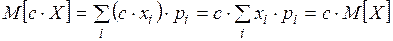 . ■
. ■
3. Рассмотрим две СВ, заданные рядом распределения:
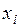 | 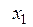 | 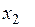 | 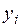 | 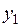 | 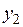 | |
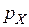 | 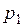 | 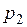 | 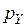 | 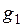 | 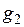 |
Составим новую СВ 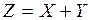 :
:
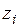 | 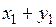 | 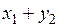 | 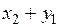 | 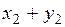 |
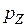 | 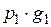 | 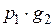 | 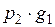 | 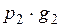 |
Проверим 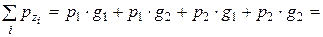
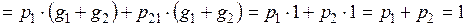
Найдём математическое ожидание:
■ 
4. Рассмотрим две независимые СВ, заданные рядом распределения:
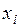 | 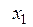 | 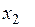 | 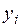 | 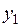 | 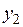 | |
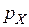 | 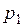 | 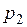 | 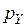 | 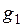 | 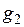 |
Составим новую СВ 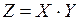 :
:
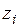 | 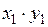 | 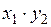 | 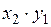 | 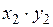 |
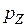 | 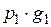 | 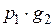 | 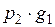 | 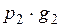 |
Проверим 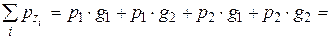
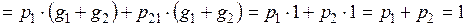
Воспользуемся формулой для вычисления математического ожидания:
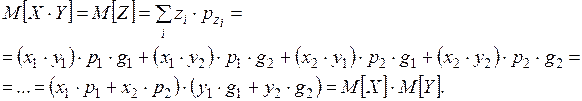
■
IV. Средняя величина – 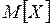 – это абстрактная характеристика распределения СВ. Значения СВ всегда колеблются около своего среднего значения. Это явление называют рассеиванием СВ. Но
– это абстрактная характеристика распределения СВ. Значения СВ всегда колеблются около своего среднего значения. Это явление называют рассеиванием СВ. Но 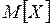 не даёт представления о том, как отдельные значения СВ сосредоточены вокруг неё. Рассеивание СВ определяет непредсказуемость принимаемых значений СВ, показателем которой является степень отклонения СВ от её математического ожидания.
не даёт представления о том, как отдельные значения СВ сосредоточены вокруг неё. Рассеивание СВ определяет непредсказуемость принимаемых значений СВ, показателем которой является степень отклонения СВ от её математического ожидания.
Центрированной СВ 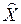 , соответствующей СВ X, называется отклонение величины от своего математического ожидания:
, соответствующей СВ X, называется отклонение величины от своего математического ожидания: 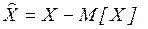 .
.
Закон распределения центрированной СВ совпадает с законом распределения самой СВ. При этом кривая распределения становится "симметричной" относительно оси OY.
Дисперсией СВ X (обозначение: 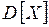 ),называется математическое ожидание квадрата центрированной СВ
),называется математическое ожидание квадрата центрированной СВ 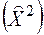 :
: 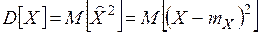 :
:
| в случае дискретной СВ | в случае непрерывной СВ |
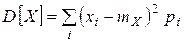 | 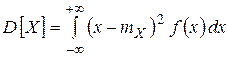 |
Дисперсия является мерилом надёжности математического ожидания. Чем меньше дисперсия, тем лучше математическое ожидание отражает собой всё распределение СВ.
Воспользуемся свойствами математического ожидания для дисперсии: 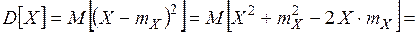
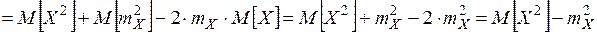
Получили формулу связи дисперсии и математического ожидания СВ:
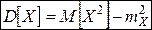
Пример.
Рассмотрим две СВ, заданные своим рядом распределения:
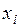 | 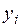 | 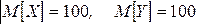 | |||||
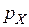 | 0,5 | 0,5 | 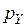 | 0,5 | 0,5 | но!!! 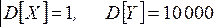 |
 2015-03-20
2015-03-20 2357
2357








