Предельные теоремы устанавливают связь между теоретическими и экспериментальными характеристиками СВ при большом числе испытаний.
¨  Неравенство Чебышева
Неравенство Чебышева
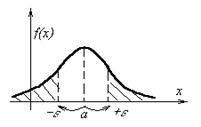
Вероятность того, что отклонение СВ от своего математического ожидания 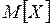 будет по абсолютной величине не меньше любого положительного числа
будет по абсолютной величине не меньше любого положительного числа 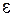 , ограничена сверху величиной
, ограничена сверху величиной 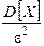 (где
(где 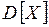 – дисперсия СВ):
– дисперсия СВ):
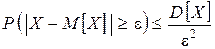
| или 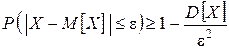
|
► 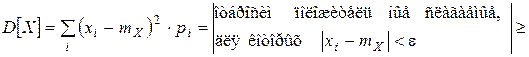
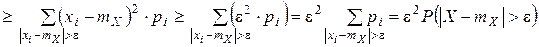
Откуда получим: 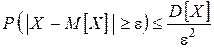 ■
■
· Из неравенства Чебышева следует, что, чем меньше дисперсия, тем меньше вероятность отклонения СВ от своего математического ожидания.
Неравенство Чебышева может использоваться только для относительно больших 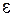 .
.
например:
1) 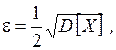 тогда
тогда 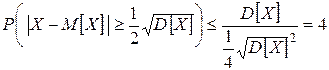
– такая оценка не представляет интерес 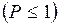 .
.
2) 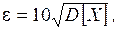
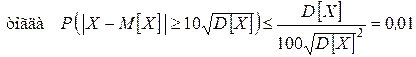
¨ Теорема Чебышева
При неограниченном увеличении числа независимых испытаний среднее арифметическое наблюдавшихся значений СВ, сходится по вероятности к её математическому ожиданию:
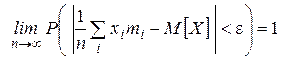
|
где 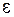 – сколь угодно малое положительное число.
– сколь угодно малое положительное число.
► Пусть в 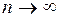 испытаниях значение
испытаниях значение 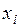 появилось
появилось 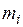 число раз (
число раз (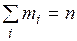 ).
).
Рассмотрим среднее арифметическое наблюдённых значений СВ:
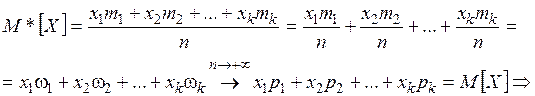
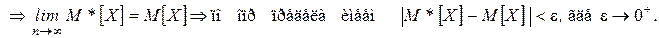
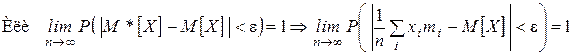 ■
■
¨ Обобщённая теорема Чебышева
Если последовательность попарно независимых СВ X1, X2, …, Xn имеет конечные математические ожидания и дисперсии этих величин не превышают постоянного числа С, то среднее арифметическое СВ сходится по вероятности к среднему арифметическому их математических ожиданий:
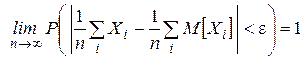
| или 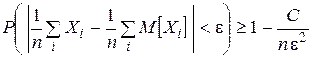
|
где 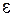 – сколь угодно малое положительное число.
– сколь угодно малое положительное число.
►Имеем последовательность СВ: X1, X2, …, Xn.
Среднее арифметическое СВ есть СВ 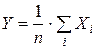
Для неё 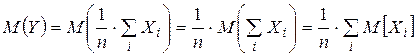 ,
,
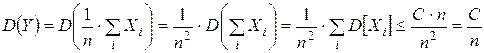 .
.
Применим к СВ 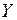 неравенство Чебышева:
неравенство Чебышева: 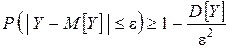
Т.е. 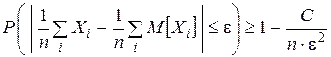 . Но
. Но 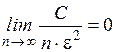 .
.
Следовательно, учитывая что 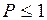 :
: 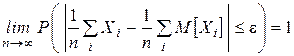 ■
■
· Если в n испытаниях значение СВ Xi повторяется ni раз (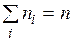 ), то:
), то:
1. среднее арифметическое СВ: 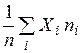 ;
;
2. среднее арифметическое математических ожиданий СВ: 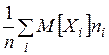 .
.
Следствие. Если результаты измерений независимы, при этом совокупность СВ X1, X2,..,Xn имеет одно то же математическое ожидание (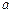 ) и дисперсии этих величин ограничены одной той же константой (С), то
) и дисперсии этих величин ограничены одной той же константой (С), то 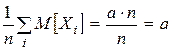 . Тогда:
. Тогда:
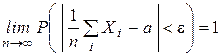
| или 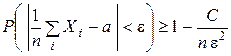
|
где 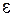 – сколь угодно малое положительное число.
– сколь угодно малое положительное число.
¨ Теорема Бернулли
При неограниченном увеличении числа независимых испытаний частота события А (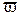 ) сходится по вероятности к вероятности его появления в одном испытании
) сходится по вероятности к вероятности его появления в одном испытании 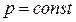 :
:
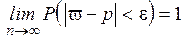
| или 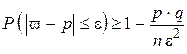
|
где 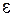 – сколь угодно малое положительное число.
– сколь угодно малое положительное число.
►Пусть производится n независимых испытаний. В каждом из них событие А может наступить с вероятностью 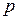 . СВ
. СВ 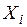 – число появления события А в
– число появления события А в 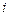 –ом опыте.
–ом опыте.
Каждая ДСВ 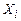 имеет закон распределения: имеет закон распределения:
| 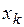
| ||
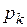
| 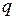
| 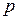
|
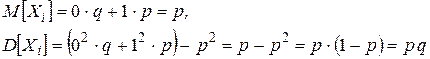
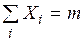 – число появления события А в n испытаниях.
– число появления события А в n испытаниях.
Составим СВ: 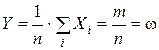 – частота появления события А в n испытаниях.
– частота появления события А в n испытаниях.
Для неё 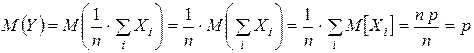 ,
,
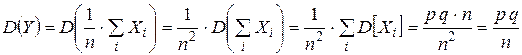 .
.
Применим к СВ 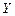 неравенство Чебышева:
неравенство Чебышева: 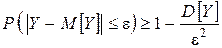 .
.
Т.е. 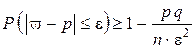 .
.
Но 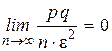 . Следовательно, учитывая что
. Следовательно, учитывая что 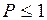 :
: 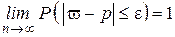 ■
■
¨ Теорема Пуассона
Если производится n независимых испытаний и вероятность появления события А в i-ом опыте равна 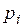 , то при увеличении n частота события А появления в одном испытании сходится по вероятности к среднему арифметическому вероятностей
, то при увеличении n частота события А появления в одном испытании сходится по вероятности к среднему арифметическому вероятностей 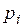 :
:
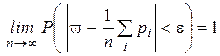
| или 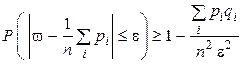
|
где 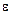 – сколь угодно малое положительное число.
– сколь угодно малое положительное число.
¨ Центральная предельная теорема – теорема Ляпунова
Если СВ X1, X2, …, Xn попарно независимы и имеют один и тот же закон распределения с математическим ожиданием m и дисперсией 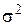 , причём существует третий абсолютный момент, то при неограниченном увеличении n закон распределения суммы
, причём существует третий абсолютный момент, то при неограниченном увеличении n закон распределения суммы 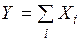 неограниченно приближается к нормальному, где имеет место равенство:
неограниченно приближается к нормальному, где имеет место равенство:
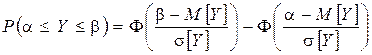
|
Где 1. 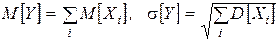
2. 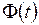 – функция Лапласа (табулирована).
– функция Лапласа (табулирована).
¨ Теорема Муавра–Лапласа
Если производится n независимых испытаний, в каждом из которых событие А появляется с вероятностью 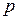 , то для любого интервала
, то для любого интервала 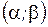 справедливо соотношение:
справедливо соотношение:
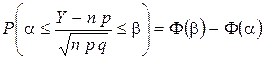
| или 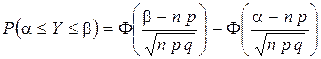
|
 2015-03-20
2015-03-20 394
394








