I. БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ СВ
Для дискретной СВ X, которая является числом появления события А в n –независимых испытаниях, в каждом из которых событие А может наступить с постоянной вероятностью p (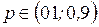 ), работает биномиальный закон распределения, определяемый формулой Бернулли: ), работает биномиальный закон распределения, определяемый формулой Бернулли:
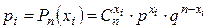
| Многоугольник распределения
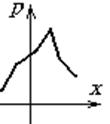
|
Найдём математическое ожидание.
Продифференцируем бином Ньютона 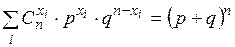 по переменной
по переменной 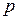
и умножим обе части равенства на 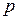 :
:
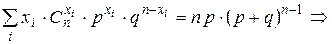
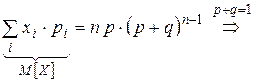
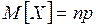
Найдём дисперсию.
Дважды продифференцируем бином Ньютона 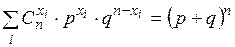 по переменной
по переменной 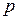 и умножим обе части равенства на
и умножим обе части равенства на 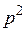 :
:
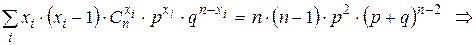
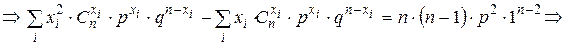
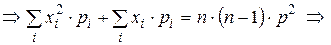
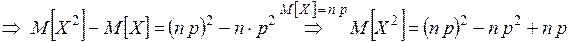 .
.
Тогда 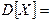
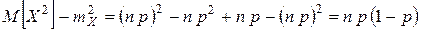
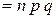 .
.
Замечание: при большом значении 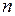 для вычисления
для вычисления 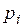 применяют локальную формулу Муавра–Лапласа
применяют локальную формулу Муавра–Лапласа 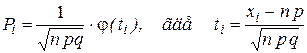 .
.
II. РАСПРЕДЕЛЕНИЕ ПУАССОНА
Для дискретной СВ X, которая является числом появления события А в n –независимых испытаниях (где n →+∞), в каждом из которых событие А может наступить с постоянной вероятностью p (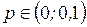 ), работает закон распределения Пуассона, определяемый формулой: ), работает закон распределения Пуассона, определяемый формулой: 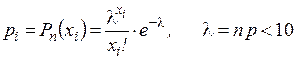
| Многоугольник
распределения
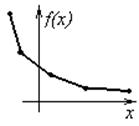
|
Найдём математическое ожидание.
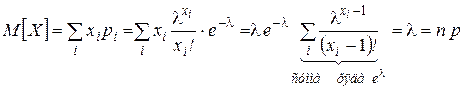 . Т.о. получили
. Т.о. получили 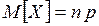 .
.
Найдём дисперсию.
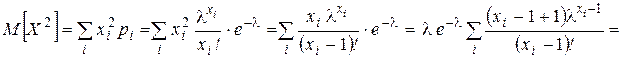
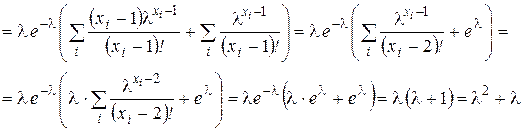
Тогда 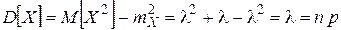
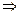
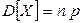 .
.
 2015-03-20
2015-03-20 521
521








