I. РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ СВ
Непрерывная СВ X имеет равномерное распределение на интервале 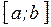 , если на нём плотность распределения
, если на нём плотность распределения  постоянна, а вне его – равна нулю:
постоянна, а вне его – равна нулю:
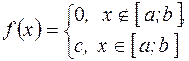
Найдём дифференциальную функцию распределения СВ.
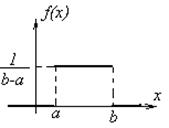 По свойствам дифференциальной функции имеем
По свойствам дифференциальной функции имеем 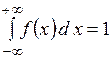 .
.
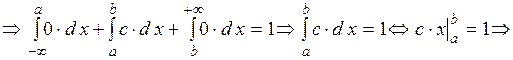
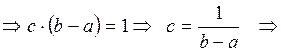
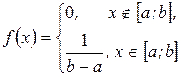
Найдём интегральную функцию распределения СВ.
1) 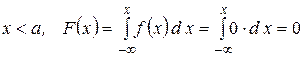 .
.
2) 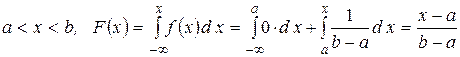 .
.
3) 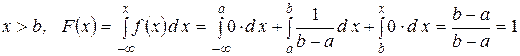 .
.
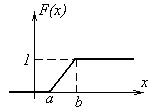 В итоге
В итоге 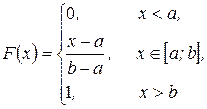
Найдём математическое ожидание.
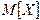
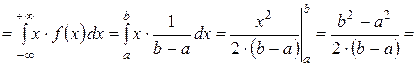
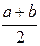 .
.
Найдём дисперсию.
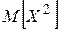
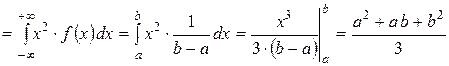 .
.
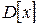
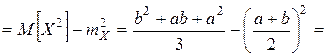
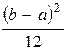 .
.
Найдём интервальную вероятность.
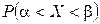
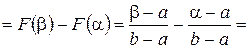
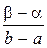 , где
, где 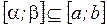 .
.
II. ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ СВ
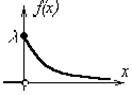 Непрерывная СВ X имеет показательное распределение, если плотность распределения
Непрерывная СВ X имеет показательное распределение, если плотность распределения  подчинена закону:
подчинена закону:
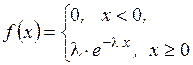
Найдём интегральную функцию распределения СВ.
1) 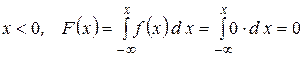
2) 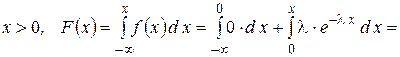
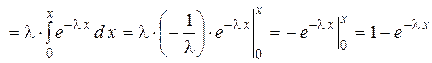
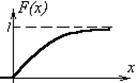 В итоге
В итоге 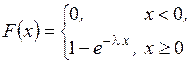
Найдём математическое ожидание.
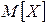
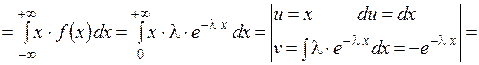
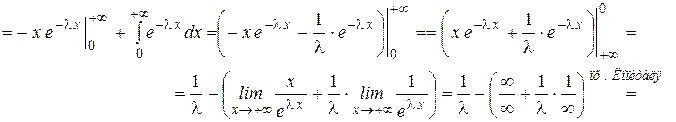
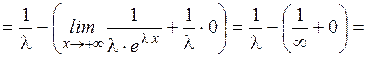
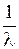
Найдём дисперсию.
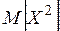
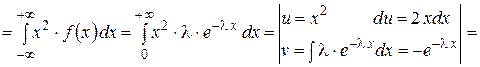
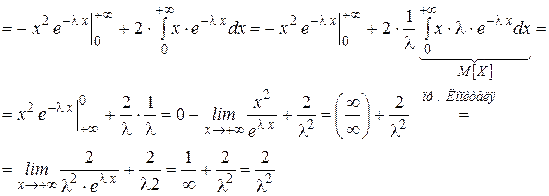
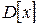
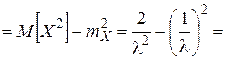
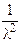
Найдём интервальную вероятность.
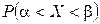
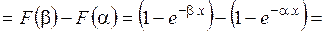
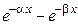 , где
, где 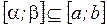
III. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ СВ (ЗАКОН ГАУССА)
– занимает центральное место, т.к. он является предельным законом, к которому приближаются другие законы распределения СВ.
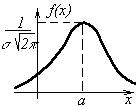 Непрерывная СВ X имеет нормальное распределение, если плотность распределения
Непрерывная СВ X имеет нормальное распределение, если плотность распределения 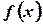 подчинена закону:
подчинена закону:
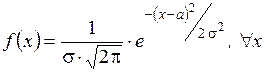
Найдём интегральную функцию распределения СВ.
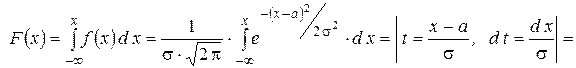
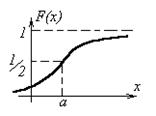
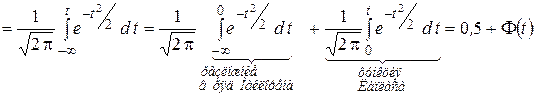
В итоге 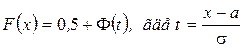
Найдём математическое ожидание.
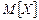
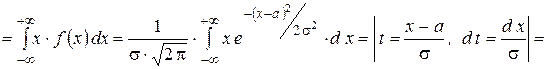
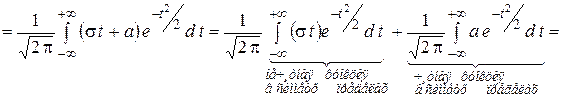
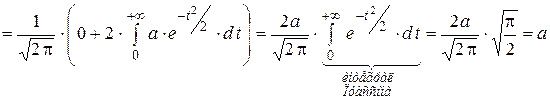
Следовательно, константа 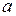 в формуле дифференциальной функции есть математическое ожидание данной СВ:
в формуле дифференциальной функции есть математическое ожидание данной СВ: 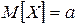
Найдём дисперсию.
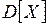
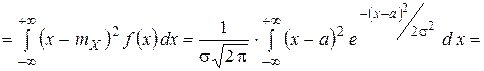
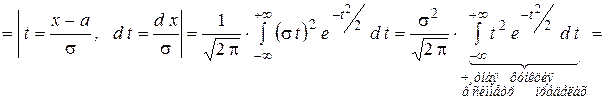
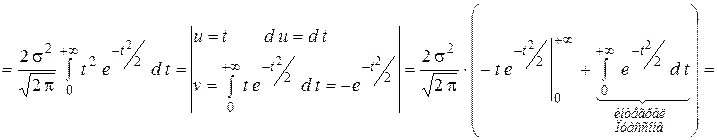
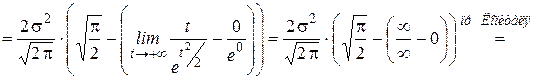
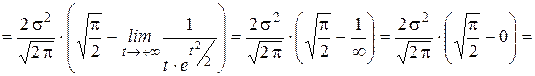
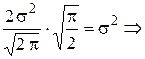
константа 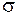 в формуле дифференциальной функции есть среднее квадратическое отклонение:
в формуле дифференциальной функции есть среднее квадратическое отклонение: 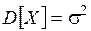 .
.
Найдём интервальную вероятность.
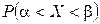
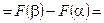
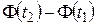 , где
, где 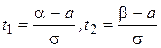
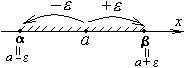 Замечания:
Замечания:
1. Для симметричного относительно 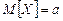 интервала имеем:
интервала имеем:
Тогда 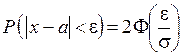
2. 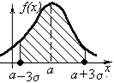 Определим
Определим 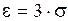 и найдём
и найдём
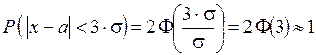
Получили правило «трёх сигм»:
Практически все значения СВ, распределённой по нормальному закону, попадают в интервал 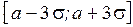 .
.
3. 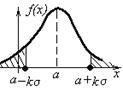 Найдём вероятность "односторонней" ошибки – слишком сильного отклонения от среднего в одну сторону.
Найдём вероятность "односторонней" ошибки – слишком сильного отклонения от среднего в одну сторону.
Учитывая симметрию графика функции, имеем:
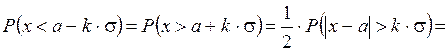
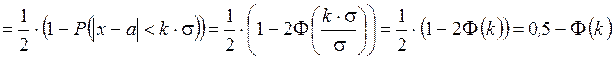
 2015-03-20
2015-03-20 588
588








