Уравнение данной модели имеет вид: 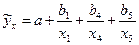 .
.
Для оценивания параметров модели проводят замену переменных:
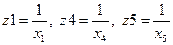 .
.
Получим уравнение множественной линейной регрессии:
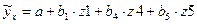 .
.
Для построения уравнения используем данные таблицы (рисунок 4.9):
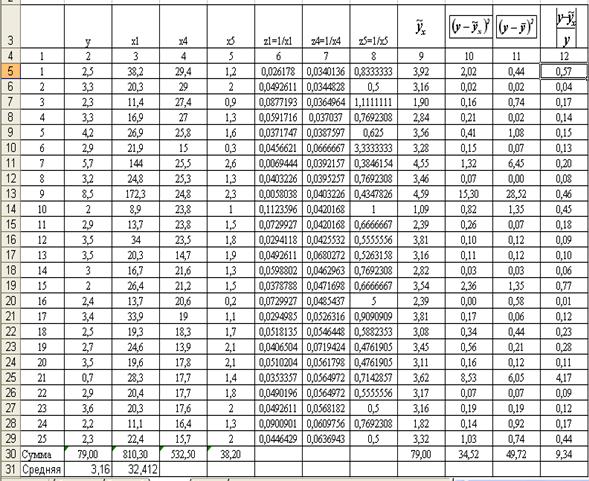
Рисунок 4.9 – Исходные данные для построения гиперболической модели
Результаты регрессионного анализа представлены на рисунке 4.10.
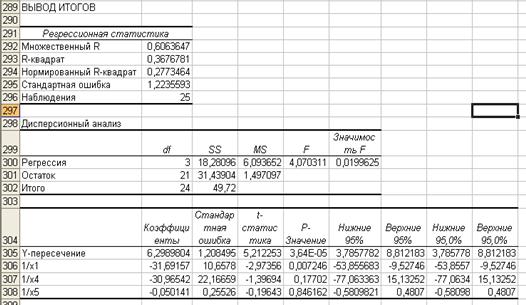
Рисунок 4.10 – Результат применения инструмента Регрессия
Получено уравнение множественной линейной регрессии: 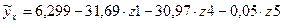 .
.
Оценивая параметры данного уравнения, замечаем, что статистически значимым является параметр при X1, (об этом свидетельствует величина р – значение из рисунка 4.10) следовательно, целесообразно строить уравнение гиперболической регрессии только с данным фактором. В результате получаем равнение следующего вида: 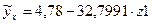 (рисунок 4.11).
(рисунок 4.11).
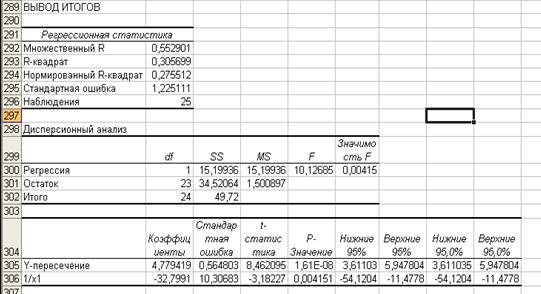
Рисунок 4.11 – Результат применения инструмента Регрессия
Следовательно, получим уравнение регрессии: 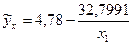 .
.
Подставляя в данное уравнение фактические значения x1, получаем теоретические значения результата 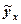 (рисунок 4.9 графа 9). По ним рассчитаем показатели:
(рисунок 4.9 графа 9). По ним рассчитаем показатели:
- индекс корреляции составит (рисунок 4.9): 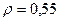 - связь между признаками средняя;
- связь между признаками средняя;
- средняя ошибка аппроксимации (рисунок 4.9, графа 12)
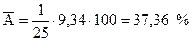 ;
;
- F-критерий 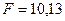 (рисунок 4.9).
(рисунок 4.9).
Данная модель также статистически значима и имеет удовлетворительное качество.
 2015-03-20
2015-03-20 919
919

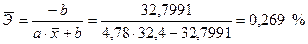 ;
;






