Приращением функции 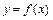 в точке
в точке 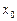 , соответствующим приращению аргумента
, соответствующим приращению аргумента 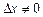 называется выражение
называется выражение 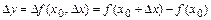 .
.
Производной 1-ого порядка функции 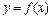 в точке
в точке 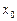 называется конечный предел
называется конечный предел 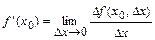 .
.
Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Необходимым условием дифференцируемости в точке является непрерывность функции в данной точке.
Любая элементарная функция 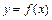 дифференцируема во всякой внутренней точке
дифференцируема во всякой внутренней точке 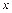 естественной области определения
естественной области определения 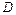 функции
функции 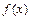 , в которой аналитическое выражение её производной
, в которой аналитическое выражение её производной 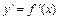 имеет смысл. Производная
имеет смысл. Производная 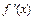 , рассматриваемая на множестве тех точек
, рассматриваемая на множестве тех точек 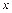 , где она существует, сама является функцией. Операция нахождения производной
, где она существует, сама является функцией. Операция нахождения производной 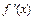 называется также дифференцированием функции
называется также дифференцированием функции 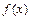 .
.
 2015-03-20
2015-03-20 270
270








