Комплексным числом называется число вида 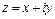 , где
, где 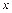 ,
, 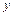 -действительные числа, символ
-действительные числа, символ 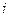 - мнимая единица, для которой
- мнимая единица, для которой 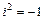 . Число
. Число 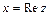 - называется действительной частью комплексного числа
- называется действительной частью комплексного числа 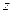 , число
, число 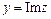 - мнимой частью. Множество всех комплексных чисел обозначается
- мнимой частью. Множество всех комплексных чисел обозначается 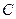 .
.
Комплексное число 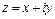 изображается на плоскости с системой координат
изображается на плоскости с системой координат 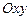 (называемой комплексной плоскостью) точкой, обозначаемой той же буквой
(называемой комплексной плоскостью) точкой, обозначаемой той же буквой 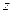 и имеющей координаты
и имеющей координаты 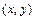 .
.
Комплексное число на комплексной плоскости изображается также радиус-вектором точки 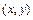 . Длина радиус-вектора называется модулем комплексного числа:
. Длина радиус-вектора называется модулем комплексного числа: 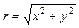 , а угол его
, а угол его 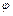 с осью
с осью 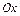 называется аргументом комплексного числа:
называется аргументом комплексного числа: 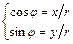 ,
, 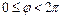 .
.
Аргумент 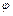 комплексного числа вычисляют, как правило, по формуле:
комплексного числа вычисляют, как правило, по формуле: 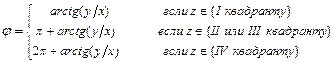 .
.
Комплексно-сопряжённым числу 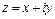 называется число
называется число 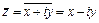 .
.
Представление комплексного числа выражением 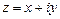 называется алгебраической формой комплексного числа, выражением
называется алгебраической формой комплексного числа, выражением 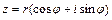 - тригонометрической формой ивыражением
- тригонометрической формой ивыражением 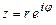 - его показательной формой.
- его показательной формой.
Арифметические действия (сложение, вычитание, умножение) над комплексными числами в алгебраической форме выполняют по правилам действий над многочленами, с учётом того, что 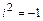 :
:
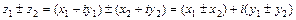 ;
;
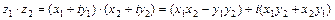 .
.
Деление комплексных чисел выполняют по формуле: 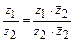 .
.
Умножение и деление комплексных чисел в тригонометрической форме выполняют по формулам:
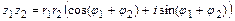 ;
;
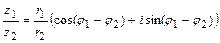 .
.
Умножение и деление комплексных чисел в показательной форме выполняют по формулам: 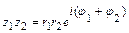 ;
; 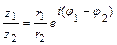 .
.
Возведение комплексного числа 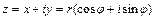 в натуральную степень
в натуральную степень 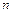 выполняют, используя формулу Муавра:
выполняют, используя формулу Муавра: 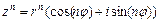 .
.
Извлечение корня 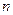 -ой степени из комплексного числа
-ой степени из комплексного числа 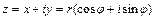 (не равного нулю) выполняют по формуле:
(не равного нулю) выполняют по формуле:
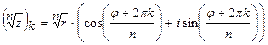 ,
, 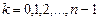
(здесь 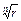 - действительное положительное число). Корень степени
- действительное положительное число). Корень степени 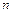 из комплексного числа имеет
из комплексного числа имеет 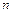 различных значений, расположенных на комплексной плоскости на окружности радиуса
различных значений, расположенных на комплексной плоскости на окружности радиуса 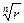 .
.
Алгебраическим многочленом степени 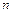 называется выражение вида:
называется выражение вида: 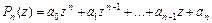 , где
, где 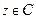 ,
, 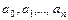 - некоторые числа (вообще говоря, комплексные), называемые коэффициентами многочлена, причём
- некоторые числа (вообще говоря, комплексные), называемые коэффициентами многочлена, причём 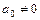 .
.
Алгебраическим уравнением степени 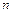 называется уравнение вида
называется уравнение вида 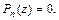 Число
Число 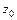 , для которого
, для которого 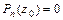 называется корнем многочлена или уравнения.
называется корнем многочлена или уравнения.
Теорема Безу. Число 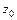 является корнем многочлена
является корнем многочлена 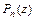 тогда и только тогда, когда
тогда и только тогда, когда 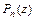 делится на
делится на 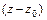 , т.е. когда
, т.е. когда 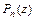 представляется в виде:
представляется в виде: 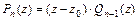 , где
, где 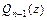 - многочлен степени
- многочлен степени 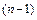 .
.
Число 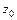 называется корнем кратности
называется корнем кратности 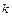 многочлена
многочлена 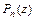 , если
, если 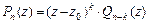 , где
, где 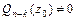 .
.
Для многочленов имеет место следующая теорема:
Теорема Гаусса (основная теорема алгебры).Всякий многочлен ненулевой степени 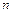 имеет ровно
имеет ровно 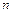 корней, если каждый корень считать ровно столько раз, какова его кратность.
корней, если каждый корень считать ровно столько раз, какова его кратность.
Всякий многочлен 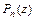 с действительными коэффициентами всегда можно разложить в произведение линейных и квадратичных (с действительными коэффициентами) множителей.
с действительными коэффициентами всегда можно разложить в произведение линейных и квадратичных (с действительными коэффициентами) множителей.
Всякий квадратный многочлен с действительными коэффициентами 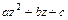 на множестве комплексных чисел всегда можно разложить в произведение только линейных множителей:
на множестве комплексных чисел всегда можно разложить в произведение только линейных множителей: 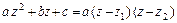 , где корни
, где корни 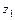 и
и 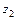 многочлена находятся по формулам:
многочлена находятся по формулам:
1) если 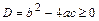 , то
, то 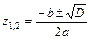 - действительные;
- действительные;
2) если 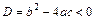 , то
, то 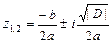 - комплексно-сопряжённые.
- комплексно-сопряжённые.
4.275. Изобразить на комплексной плоскости числа:
а) 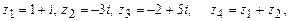
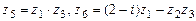 ;
;
б) 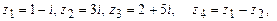
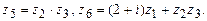
В задачах 4.276- 4.279 выполнить указанные действия, представив результат в алгебраической форме:
4.276 а) 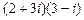 ; б)
; б) 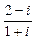 ; в)
; в) 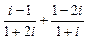 .
.
4.277 а) 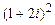 ; б)
; б) 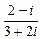 ; в)
; в) 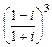 .
.
4.278
а) 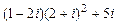 ; б)
; б) 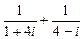 ; в)
; в) 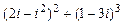 .
.
4.279
а) 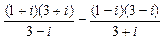 ; б)
; б) 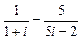 ; в)
; в) 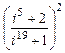 .
.
В задачах 4.280- 4.283 представить в тригонометрической форме комплексные числа, заданные в алгебраической форме:
4.280 а) 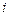 ; б)
; б) 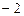 ; в)
; в) 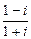 .
.
4.281 а) 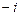 ; б)
; б) 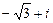 ; в)
; в) 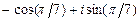 .
.
4.282 а) 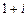 ; б)
; б) 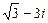 ; в)
; в) 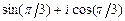 .
.
4.283
а) 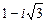 ; б)
; б) 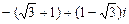 ; в)
; в) 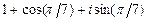 .
.
4.284 Вычислить:
а) 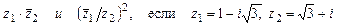 ;
;
б) 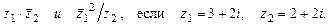
В задачах 4.285-4.286 представить в показательной форме следующие комплексные числа:
4.285 а) 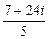 ; б)
; б) 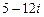 ; в)
; в) 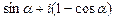 .
.
4.286 а) 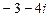 ; б)
; б) 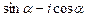 ; в)
; в) 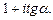
4.287 Данные числа 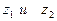 представить в показательной форме и выполнить указанные действия над ними:
представить в показательной форме и выполнить указанные действия над ними:
а) 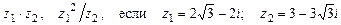 ;
;
б) 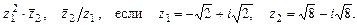
В задачах 4.288-4.289 используя формулу Муавра, вычислить следующие выражения:
4.288 а) 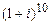 ; б)
; б) 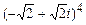 ; в)
; в) 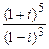 .
.
4.289 а) 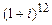 ; б)
; б) 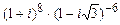 ; в)
; в) 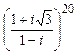 .
.
4.290 Найти и изобразить на комплексной плоскости все корни 2-й, 3-й и 4-й степени из единицы.
В задачах 4.291-4.293 найти все значения корней:
4.291 а) 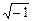 ; б)
; б) 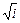 ; в)
; в) 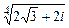 .
.
4.292 а) 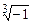 ; б)
; б) 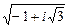 ; в)
; в) 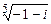 .
.
4.293 а) 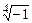 ; б)
; б) 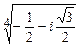 ; в)
; в) 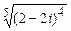 .
.
В задачах 4.294-4.296 найти все корни следующих алгебраических уравнений на множестве комплексных чисел:
4.294 а) 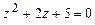 ; б)
; б) 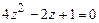 ; в)
; в) 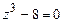 .
.
4.295 а) 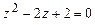 ; б)
; б) 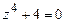 ; в)
; в) 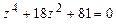 .
.
4.296 а) 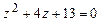 ; б)
; б) 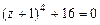 ; в)
; в) 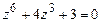 .
.
 2015-03-20
2015-03-20 760
760








