ГЛАВА 4. ВВЕДЕНИЕ В АНАЛИЗ.
Величина, сохраняющая одно и тоже числовое значение, называется постоянной. Величина, принимающая различные числовые значения, называется переменной. Функцией 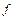 называется правило, по которому каждому числу
называется правило, по которому каждому числу 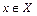 ставится в соответствие одно вполне определённое число
ставится в соответствие одно вполне определённое число 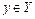 , и пишут
, и пишут 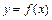 . Множество
. Множество 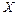 называется областью определения функции,
называется областью определения функции, 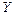 - множеством ( или областью) значений функции,
- множеством ( или областью) значений функции, 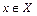 - аргументом,
- аргументом, 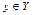 - значением функции. Наиболее распространённым способом задания функции является аналитический способ, при котором функция задаётся формулой. Естественной областью определения функции
- значением функции. Наиболее распространённым способом задания функции является аналитический способ, при котором функция задаётся формулой. Естественной областью определения функции 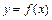 называется множество
называется множество 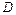 значений аргумента
значений аргумента 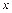 , для которого данная формула имеет смысл. Графиком функции
, для которого данная формула имеет смысл. Графиком функции 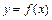 ,
, 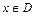 в прямоугольной системе координат
в прямоугольной системе координат 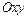 , называется множество всех точек плоскости с координатами
, называется множество всех точек плоскости с координатами 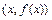 ,
, 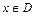 .
.
Функция 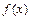 называется чётной на множестве
называется чётной на множестве 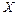 , симметричном относительно точки
, симметричном относительно точки 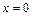 , если для всех
, если для всех 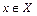 выполняется условие:
выполняется условие: 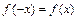 и нечётной, если выполняется условие
и нечётной, если выполняется условие 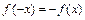 . В противном случае
. В противном случае 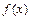 - функция общего вида или ни чётная, ни нечётная.
- функция общего вида или ни чётная, ни нечётная.
Функция 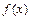 называется периодической на множестве
называется периодической на множестве 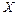 , если существует число
, если существует число 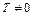 (период функции), такое, что для всех
(период функции), такое, что для всех 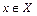 выполняется условие:
выполняется условие: 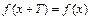 . Наименьшее число
. Наименьшее число 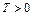 называется основным периодом.
называется основным периодом.
Функция 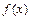 называется монотонно возрастающей (убывающей) на множестве
называется монотонно возрастающей (убывающей) на множестве 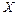 , если большему значению аргумента
, если большему значению аргумента 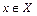 соответствует большее (меньшее) значение функции
соответствует большее (меньшее) значение функции 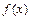 .
.
Функция 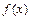 называется ограниченной на множестве
называется ограниченной на множестве 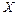 , если существует число
, если существует число 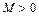 , такое, что для всех
, такое, что для всех 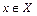 выполняется условие:
выполняется условие: 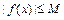 . В противном случае функция - неограниченная.
. В противном случае функция - неограниченная.
Обратной к функции 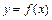 ,
, 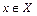 ,
, 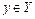 называется такая функция
называется такая функция 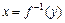 , которая определена на множестве
, которая определена на множестве 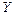 и каждому
и каждому
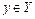 ставит в соответствие такое
ставит в соответствие такое 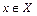 , что
, что 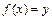 . Для нахождения функции
. Для нахождения функции 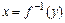 , обратной к функции
, обратной к функции 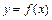 , нужно решить уравнение
, нужно решить уравнение 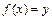 относительно
относительно 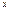 . Если функция
. Если функция 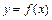 ,
, 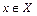 является строго монотонной на
является строго монотонной на 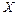 , то она всегда имеет обратную, при этом, если функция возрастает (убывает), то обратная функция также возрастает (убывает).
, то она всегда имеет обратную, при этом, если функция возрастает (убывает), то обратная функция также возрастает (убывает).
Функция 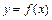 , представляемая в виде
, представляемая в виде 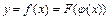 , где
, где 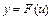 ,
, 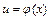 - некоторые функции такие, что область определения функции
- некоторые функции такие, что область определения функции 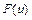 содержит всё множество значений функции
содержит всё множество значений функции 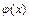 , называется сложной функцией независимого аргумента
, называется сложной функцией независимого аргумента 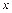 . Переменную
. Переменную 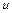 называют при этом промежуточным аргументом. Сложную функцию
называют при этом промежуточным аргументом. Сложную функцию 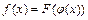 называют также композицией функций
называют также композицией функций 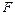 и
и 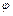 , и пишут:
, и пишут: 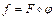 .
.
4.1 В треугольнике 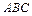 сторона
сторона 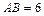 см, сторона
см, сторона 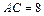 см и угол
см и угол 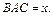 Выразить
Выразить 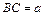 и площадь
и площадь 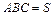 как функции переменной
как функции переменной 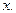
4.2 Найти выражение для площади 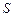 равнобочной трапеции с основаниями
равнобочной трапеции с основаниями 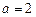 и
и 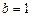 как функции угла
как функции угла 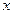 при основании
при основании 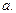
4.3 В шар радиуса R вписан цилиндр. Написать выражение для объема V цилиндра от его высоты Н. Найти область определения этой функции.
4.4 В шар радиуса R вписан прямой круговой конус. Написать выражение для площади боковой поверхности S конуса: а) от его образующей l; б) от угла 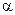 при вершине конуса в его осевом сечении; в) от угла
при вершине конуса в его осевом сечении; в) от угла 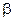 при основании конуса. Найти области определения каждой из полученных функций.
при основании конуса. Найти области определения каждой из полученных функций.
4.5 Определить функцию 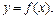 удовлетворяющую заданному условию: а)
удовлетворяющую заданному условию: а) 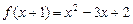 ;
;
б) 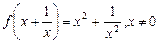 ; в)
; в) 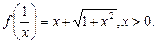
В задачах 4.6-4.12 найти область определения 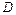 функций:
функций:
4.6 а) 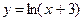 ; б)
; б) 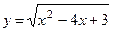 ;
;
в) 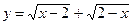 ; г)
; г) 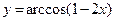 .
.
4.7 а) 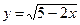 ; б)
; б) 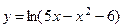 ;
;
в) 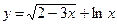 ; г)
; г) 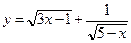 .
.
4.8 а) 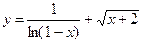 ; б)
; б) 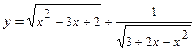 .
.
4.9 а) 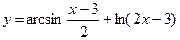 ; б)
; б) 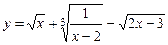 .
.
4.10 а) 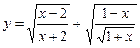 ; б)
; б) 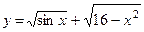 .
.
4.11 а) 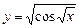 ; б)
; б) 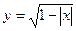 .
.
4.12 а) 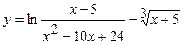 ; б)
; б) 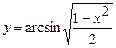 .
.
В задачах 4.13-4.21, выяснить какие из указанных функций четные, какие нечетные, а какие ни четные, ни нечетные.
4.13 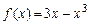 . 4.14
. 4.14 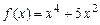 . 4.15
. 4.15 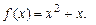
4.16 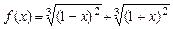 . 4.17
. 4.17 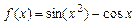 .
.
4.18 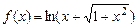 . 4.19
. 4.19 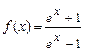 .
.
4.20 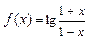 . 4.21
. 4.21 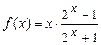 .
.
В задачах 4.22-4.30 выяснить, какие из функций являются периодическими, и определить их наименьший период Т:
4.22 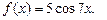 4.23
4.23 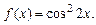 4.24
4.24 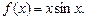
4.25 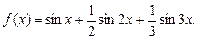 4.26
4.26 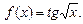
4.27 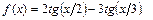 4.28
4.28 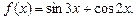
4.29 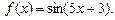 4.30
4.30 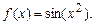
В задачах 4.31-4.34 доказать, что следующие функции являются монотонно возрастающими в указанных промежутках:
4.31 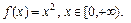 4.32
4.32 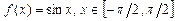 .
.
4.33  4.34
4.34 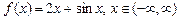 .
.
В задачах 4.35-4.38 доказать, что следующие функции являются монотонно убывающими в указанных промежутках:
4.35 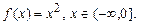 4.36
4.36 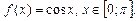
4.37 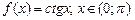 . 4.38
. 4.38 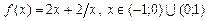 .
.
В задачах 4.39-4.46 найти обратную функцию 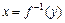 и её область определения:
и её область определения:
4.39 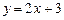 4.40
4.40 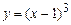 4.41
4.41 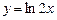 4.42
4.42 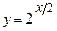
4.43 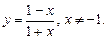 4.44
4.44 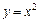 , а)
, а) 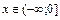 ; б)
; б) 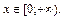
4.45 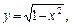 если: а)
если: а) 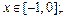 б)
б) 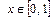 .
.
4.46 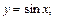 если: а)
если: а) 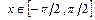 ; б)
; б) 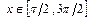 .
.
В задачах 4.47-4.51 найти композиции 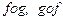 функций:
функций:
4.47 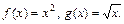 4.48
4.48 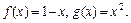
4.49 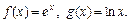 4.50
4.50 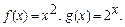
4.51 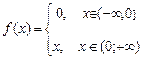 ,
, 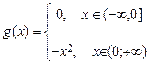 .
.
4.52 Найти 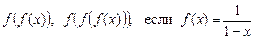 .
.
4.53 Найти 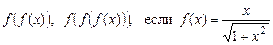 .
.
4.54 Функция 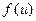 определена при
определена при 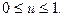 Найти области определения функций:
Найти области определения функций:
а) 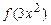 ; б)
; б) 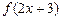 ; в)
; в) 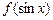 ; г)
; г) 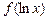 .
.
 2015-03-20
2015-03-20 725
725







