Непрерывность функций

Если функция 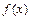определена всюду в некоторой окрестности точки 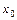(левой полуокрестности, правой полуокрестности) и 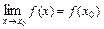(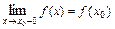, 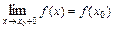), то функция 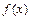называется непрерывной в точке 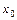(непрерывной слева, непрерывной справа).

Каждая основная элементарная функция непрерывна в каждой внутренней точке своей области определения и непрерывна слева (справа) в крайней правой (крайней левой) точке области определения.

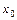
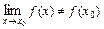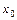Если в точке , то называется точкой разрыва функции 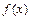. При этом различают следующие случаи:

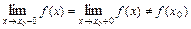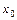1) Если , то называется точкой устранимого разрыва функции .

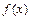2) Если в точке 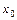функция 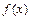имеет конечные односторонние пределы 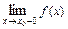и 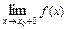, но они не равны друг другу, то 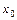называется точкой разрыва 1-ого рода.

3) В остальных случаях 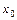называется точкой разрыва 2 -ого рода.

Функция 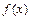называется непрерывной на отрезке 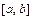, если она непрерывна в каждой его точке (в точке 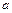- непрерывна справа, в точке 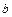- непрерывна слева). Функция 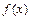непрерывная на отрезке 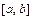обладает свойствами: 1) ограничена на 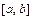; 2) достигает на отрезке 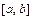своего наименьшего значения 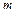и наибольшего значения 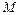; 3) для любого числа 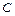, заключённого между числам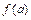и и 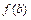, всегда найдётся точка 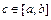такая, что 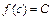; 4) если 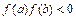, то всегда найдётся точка 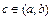такая, что .

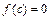В задачах 4.248-4.251 установить при каком выборе параметров, входящих в выражение функции, функция 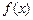будет непрерывной.

4.248 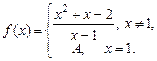4.249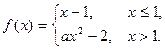

4.250 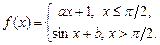4.251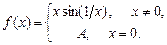

В задачах 4.252-4.269 определить точки разрыва функций и исследовать характер этих точек.

4.252 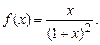4.253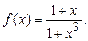

4.254 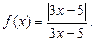4.255 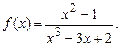4.256 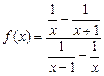. 4.257 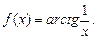4.258 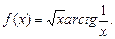4.259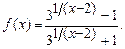

4.260 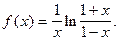4.261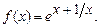

4.262 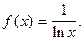4.263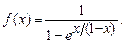

4.264 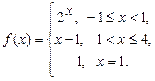4.265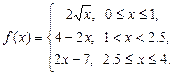

4.266 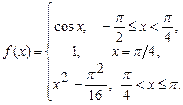4.267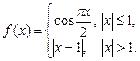

4.268 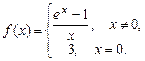4.269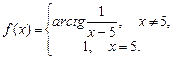

4.270 Имеет ли корень уравнение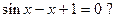

4.271 Имеет ли уравнение 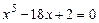корни, принадлежащие отрезку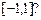

4.272 Дана функция на отрезке 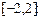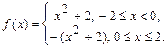Существует ли на этом отрезке точка, в которой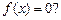

4.273 Принимает ли функция 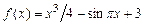значение 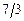внутри отрезка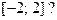

4.274 Доказать, что функция 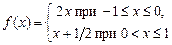разрывна в точке 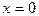и, тем не менее, принимает на 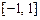как наибольшее, так и наименьшее значения.