МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ: 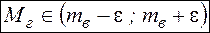
I случай (известно среднее квадратическое отклонение 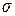 )
)
Среднее выборочное СВ 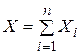 , равное
, равное 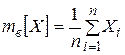 , представляет собой сумму сравнительно большого числа
, представляет собой сумму сравнительно большого числа 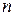 независимых величин и, согласно центральной предельной теореме, имеет распределение, близкое к нормальному. При этом:
независимых величин и, согласно центральной предельной теореме, имеет распределение, близкое к нормальному. При этом:
 (т.к.
(т.к. 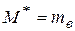 – несмещённая оценка
– несмещённая оценка 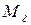 );
);
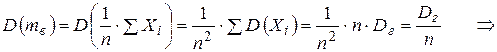
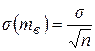 .
.
Тогда 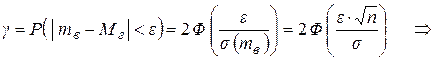
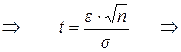
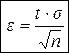 , где
, где 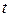 – аргумент функции Лапласа
– аргумент функции Лапласа 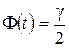 .
.
· 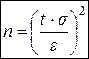 – объём выборки, необходимый для определения точности оценки
– объём выборки, необходимый для определения точности оценки 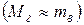 , которая не превосходит заданного значения
, которая не превосходит заданного значения 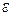 с заданным
с заданным 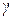 .
.
II случай (неизвестно 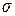 и неизвестен объёмгенеральной совокупности
и неизвестен объёмгенеральной совокупности 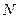 ).
).
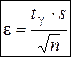 , где
, где 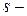 несмещённая оценка
несмещённая оценка 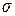 ;
;
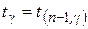 − табулировано распределением Стьюдента.
− табулировано распределением Стьюдента.
· 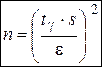 – объём выборки, необходимый для определения точности оценки
– объём выборки, необходимый для определения точности оценки 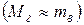 , которая не превосходит заданного значения
, которая не превосходит заданного значения 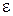 с заданным
с заданным 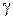 .
.
III случай (неизвестно 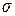 и известен объёмгенеральной совокупности
и известен объёмгенеральной совокупности 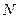 ).
).
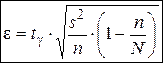 , где
, где 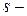 несмещённая оценка
несмещённая оценка 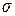 .
.
· 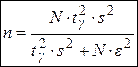 – объём выборки, необходимый для определения точности оценки
– объём выборки, необходимый для определения точности оценки 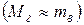 , которая не превосходит заданного значения
, которая не превосходит заданного значения 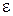 с заданным
с заданным 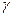 .
.
 2015-03-20
2015-03-20 440
440








