2015-03-20
912
При замене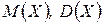 
на их точечные оценки 
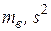совершается ошибка.
Оценить её можно с помощью вероятности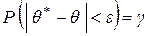 
.Чем меньше разность 
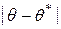, тем точнее оценка.
· Вероятность γ того, что мы не ошибёмся, если поверим оценке, построенной с помощью выборки называется уровнем доверия (надёжностью).
· Интервал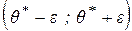 
, который покрывает неизвестный параметр 
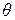с надёжностью 
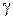, называется доверительным; 
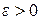– точность оценки.
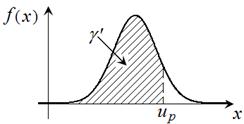
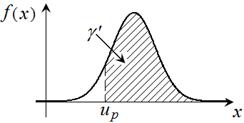
С геометрической точки зрения: доверительная вероятность 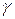 численно равна площади заштрихованной области под графиком дифференциальной функции 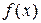 , вычисленной на интервале . |  |
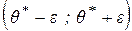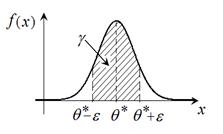Исходя из центральной предельной теоремы: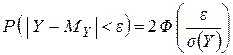 
, получаем, что чем больше надёжность (вероятность), тем больше аргумент функции Лапласа и тем больше значение 
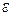(при заданном 
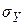). Следовательно, чем больше надёжность, тем шире доверительный интервал, тем больше вероятность ошибки, что 
.
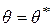2. ОДНОСТОРОННИЕ ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ
Если интерес представляет ситуация, когда важно сравнение только с одним критическим значением, то используют односторонние доверительные интервалы:
для определённого уровня доверия 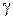строят двусторонний доверительный интервал, который затем расширяют за счёт одной из его границ.
Для двустороннего доверительного интервала: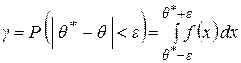 
Тогда для одностороннего доверительного интервала:
 |  |
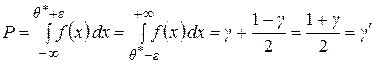
В результате получим односторонний интервал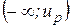 
или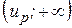 
с большей гарантией 
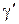. Таким образом "односторонний" подход позволяет вдвое снизить ошибку 
.
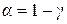· Значение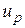 
, для которого выполняется равенство
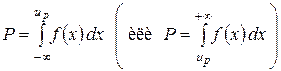называется квантилью.
