Пусть произошло 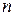 опытов.
опытов.
СВ 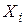 – индикатор события А в i – ом опыте:
– индикатор события А в i – ом опыте: 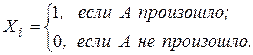
Тогда событие А произошло 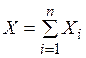 раз, и
раз, и 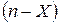 раз – оно не произошло. Частота события А выражается формулой:
раз – оно не произошло. Частота события А выражается формулой: 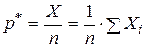 .
.
Рассмотрим частоту события как оценку вероятности 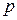 появления события.
появления события.
1) Так как опыты не зависимы, то СВ 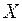 распределена по биномиальному закону с параметрами n и p. Тогда, учитывая формулу
распределена по биномиальному закону с параметрами n и p. Тогда, учитывая формулу 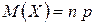 , получим:
, получим:
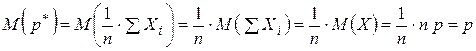
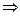
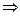
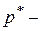 несмещённая оценка
несмещённая оценка 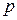 .
.
2) По теореме Бернулли имеем 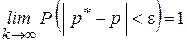
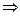
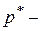 состоятельная оценка
состоятельная оценка 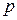 .
.
Таким образом, эмпирическая функция распределения выборки 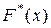 , являясь оценкой вероятности события
, являясь оценкой вероятности события 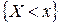 , есть несмещённая состоятельная оценка функции распределения
, есть несмещённая состоятельная оценка функции распределения 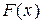 случайной величины Х.
случайной величины Х.
5. ТОЧЕЧНАЯ ОЦЕНКА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
Рассмотрим выборочную среднюю 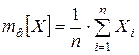 как оценку генеральной средней
как оценку генеральной средней 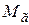 – истинного значения распределения.
– истинного значения распределения.
1) 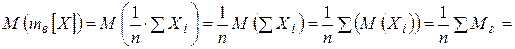
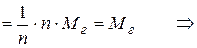
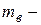 несмещённая оценка
несмещённая оценка 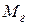 .
.
2) По теореме Чебышева имеем 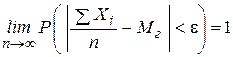
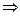
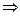
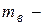 состоятельная оценка
состоятельная оценка 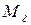 .
.
6. ТОЧЕЧНАЯ ОЦЕНКА ДИСПЕРСИИ
Рассмотрим выборочную дисперсию как оценку генеральной дисперсии 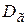 –истинного значения распределения.
–истинного значения распределения.
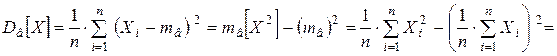
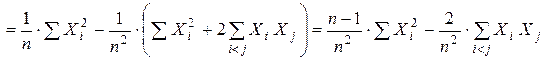
Так как статистическая дисперсия не зависит от выбора начала координат, то выберем начало координат в точке 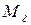 , то есть отцентрируем СВ X.
, то есть отцентрируем СВ X.
Тогда: 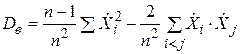 .
.
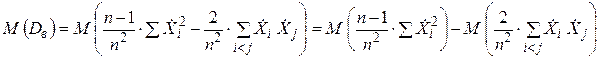
 .
.
Но 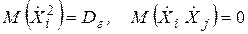 .
.
Тогда имеем 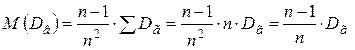
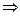
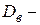 смещённая оценка
смещённая оценка 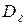 .
.
Смещение оценки произошло потому, что в формуле 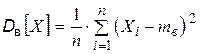 отклонение
отклонение 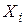 отсчитывается не от истинного математического ожидания, а от его статистического аналога
отсчитывается не от истинного математического ожидания, а от его статистического аналога 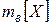 .
.
Чтобы исправить этот недостаток, вводят:
· Исправленную выборочную дисперсию – 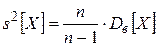 ,
,
где 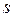 – исправленное выборочное квадратическое отклонение.
– исправленное выборочное квадратическое отклонение.
Учитывая, что 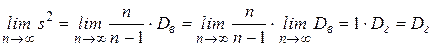 ,
,
имеем: 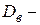 состоятельная оценка
состоятельная оценка 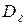 .
.
Замечание. При больших значениях п разница между 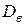 и
и 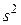 невелика и они практически равны, поэтому оценку
невелика и они практически равны, поэтому оценку 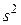 чаще используют для оценки дисперсии при малых выборках, обычно при
чаще используют для оценки дисперсии при малых выборках, обычно при 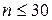 .
.
 2015-03-20
2015-03-20 2058
2058
