Основные понятия. Занимаясь гидрологическими расчетами или прогнозами, необходимо четко представлять, какая математическая модель используется для описания вероятностной

Случайные процессы

Занимаясь гидрологическими расчетами или прогнозами, необходимо четко представлять, какая математическая модель используется для описания вероятностной структуры гидрологического ряда.

До сих пор мы почти всегда подразумевали, что в качестве такой модели используется модель случайной величины. Так сорокалетний ряд среднегодовых расходов воды можно рассматривать, как сорок значений случайной величины, полученных в результате сорока природных опытов. То есть можно считать, что этот ряд представляет собой сорокалетнюю выборку из генеральной совокупности.

Если предположить, что эта выборка является репрезентативной, то по ней (на основе методов математической статистики) можно составить удовлетворительное представление обо всей генеральной совокупности, в частности – оценить параметры функции распределения.

В то же время, определить вид функции распределения по такой короткой выборке весьма сложно. Поэтому на практике, либо аналитическое выражение функции распределения задается априори, либо функция распределения выбирается из нескольких вариантов по наилучшему соответствию эмпирическим данным с использованием критериев согласия.

Опыт показывает, что большинство гидрологических величин имеет асимметричное распределение, которое хорошо аппроксимируется трехпараметрическими кривыми Крицкого-Менкеля и Пирсона III типа.

В то же время многие теоретические методы, используемые в практике гидрологических расчетов, предполагают, что случайная величина имеет нормальное распределение. Если распределение случайной величины существенно отличается от нормального, то эти методы могут приводить к значительным ошибкам.

Таким образом, недостаточно констатировать, что для описания статистической структуры ряда выбрана модель случайной величины, необходимо еще указать тип функции распределения. При этом формальный подход к выбору функции распределения также может привести к ошибкам.

Например, расходы воды – это всегда положительные величины, абсолютный максимум для которых обычно не известен; коэффициент стока изменяется от нуля до единицы; уровни воды (в зависимости от нуля графика) могут быть как положительными, так и отрицательными. Если во всех этих случаях использовать в качестве функции распределения кривую Крицкого-Менкеля, то наилучшего соответствия эмпирическим данным следует ожидать для ряда расходов воды, так как кривая Крицкого-Менкеля разработана для случайных величин с положительной асимметрией и диапазоном значений от 0 до + ∞. В двух других случаях ошибки при аппроксимации закона распределения могут быть весьма значительными.

Однако еще больше шансов совершить ошибку, если модель случайной величины в принципе не подходит для описания вероятностной структуры гидрологического ряда. Такая ситуация возникает когда имеет значение фактор времени, а следовательно и последовательность значений в ряде наблюдений.

Модель случайной величины этого не учитывает. В рамках модели случайной величины время выступает в качестве формального счетчика опытов.

Для описания временных последовательностей используется аппарат теории случайных процессов.

Теорией случайных процессов называется математическая наука, изучающая закономерности случайных явлений в динамике их развития.

Поясним это на следующем примере. Рассмотрим гидрографы для конкретного створа некоторой условной реки за 1971 – 1975 годы.

Каждый из пяти гидрографов представляет собой функцию времени на интервале один год, которую можно рассматривать как реализацию случайного процесса (рис. 6.1). В данном случае мы имеем 5 гидрографов, но очевидно, что их может быть сколько угодно.

Совокупность всех реализаций дает полное представление о случайном процессе.

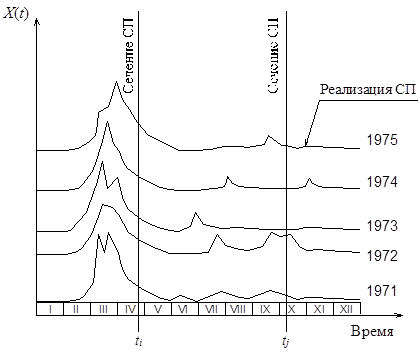
Рис.6.1. Гидрографы за 1971 – 1975 годы – как набор реализаций случайного процесса.

Если рассматривать произвольный момент времени t = t_i, то значения расходов в момент t_i по всем реализациям образуют сечение случайного процесса. При этом для любого сечения расход – есть случайная величина.

В каждом сечении случайная величина может иметь свою функцию распределения. В частности математическое ожидание и дисперсия могут быть различными в разных сечениях. В нашем примере как раз наблюдается такая ситуация, Средний многолетний расход за 15 марта будет, например, существенно выше среднего многолетнего расхода за 15 июля.

В рассмотренном примере мы имели дело с реализациями конечной длины. В общем случае длина реализаций может быть и бесконечной. Если вернуться к примеру со среднегодовыми расходами воды, то сорокалетний ряд можно рассматривать, как часть одной бесконечной реализации. Эта реализация к тому же будет единственной.

Сформулируем теперь ряд определений.

Случайным процессом X (t) называется процесс, значение которого при любом фиксированном t = t_i является случайной величиной X (t_i).

Реализацией случайного процесса X (t) называется неслучайная функция x (t), в которую превращается случайный процесс X (t) в результате опыта.

Случайная величина X (t_i), в которую обращается случайный процесс при t = t_i называется сечением случайного процесса, соответствующим данному значению аргумента.

В настоящее время наряду с термином случайный процесс используется термин случайная функция. Хотя в ряде работ эти термины используются как синонимы, автору настоящей работы ближе точка зрения, в соответствии с которой, термин случайная функция трактуется как более общий. В качестве аргумента случайной функции может фигурировать любая переменная, а под случайным процессом будем подразумевать только случайную функцию времени.

6.2. Классификация случайных процессов "по времени" и "по состояниям"

Случайный процесс X (t) называется процессом с дискретным временем, если система, в которой он протекает, может менять свои состояния только в моменты t ₁, t ₂, … t_{j ,}…, число которых конечно или счетно.

Случайный процесс X (t) называется процессом с непрерывным временем, если переходы системы из состояния в состояние могут происходить в любой момент t наблюдаемого периода.

Случайный процесс X (t) называется процессом с непрерывными состояниями, если его сечение в любой момент t представляет собой не дискретную, а непрерывную (или смешанную) величину.

Случайный процесс X (t) называется процессом с дискретными состояниями, если в любой момент времени t множество его состояний конечно или счетно; другими словами, если его сечение в любой момент t характеризуется дискретной случайной величиной.

Таким образом, все случайные процессы можно разделить на четыре класса:

1. Процессы с дискретными состояниями и дискретным временем.

2. Процессы с дискретными состояниями и непрерывным временем.

3. Процессы с непрерывными состояниями и дискретным временем.

4. Процессы с непрерывными состояниями и непрерывным временем.

Большинство гидрологических процессов являются процессами с непрерывными состояниями и непрерывным временем. Например, расход воды может изменяться в любой момент времени и принимать любые значения из некоторого интервала, границы которого зависят от размера реки и климатических особенностей региона.

При этом надо учитывать, что на практике расходы воды осредняют за некоторый интервал времени (год, месяц, сутки и т. д.). Вводя шаг дискретности по времени, мы заменяем процесс с непрерывным временем на процесс с дискретным временем. При этом в принципе, процесс остается непрерывным по состояниям.

Таким образом, производя измерения гидрологических процессов, мы чаще всего используем модель случайного процесса с дискретным временем и непрерывными состояниями.

Однако в гидрометеорологии используются и другие модели. Так процесс количественного изменения облачности обычно представляют в виде процесса с дискретным временем и дискретными состояниями, так как наблюдения за облаками производятся в фиксированные сроки, а их количество округляется до целых баллов (по десятибальной шкале).