Асимптотой графика функции 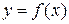 называется прямая, обладающая тем свойством, что расстояние от точки
называется прямая, обладающая тем свойством, что расстояние от точки 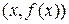 до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Различают вертикальные (рис. 4а), горизонтальные (рис. 4б) и наклонные (рис. 4в) асимптоты.
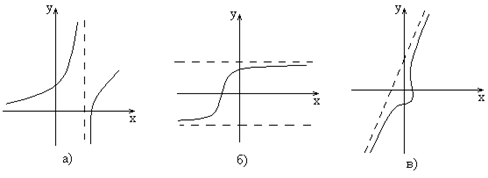
Рис. 4.
Теорема. В точках вертикальных асимптот (например, 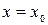 ) функция
) функция 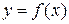 терпит разрыв, ее предел слева и справа от точки
терпит разрыв, ее предел слева и справа от точки 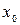 равен
равен 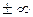 :
: 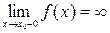 и (или)
и (или) 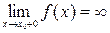 .
.
Теорема. Пусть функция 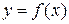 определена при достаточно больших
определена при достаточно больших 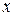 и существуют конечные пределы
и существуют конечные пределы 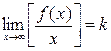 и
и 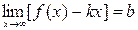 . Тогда прямая
. Тогда прямая 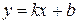 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции 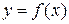 .
.
Теорема. Пусть функция 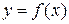 определена при достаточно больших
определена при достаточно больших 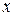 и существует предел функции
и существует предел функции 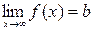 . Тогда прямая
. Тогда прямая 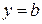 есть горизонтальная асимптота графика функции
есть горизонтальная асимптота графика функции 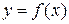 .
.
Горизонтальная асимптота является частным случаем наклонной асимптоты, когда 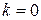 . Поэтому, если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
. Поэтому, если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
Пример. Найти асимптоты графика функции 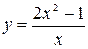 .
.
 2015-03-20
2015-03-20 985
985








