Функция 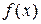 называется выпуклой вниз (выпуклой вверх) на промежутке
называется выпуклой вниз (выпуклой вверх) на промежутке 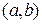 , если для любых значений
, если для любых значений 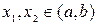 выполняется неравенство
выполняется неравенство 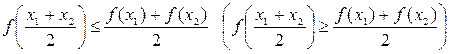 .
.
Теорема (достаточное условие выпуклости функции). Если функция 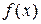 имеет на интервале
имеет на интервале 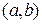 вторую производную
вторую производную 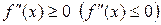 , то график функции имеет на
, то график функции имеет на 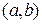 выпуклость направленную вниз (вверх).
выпуклость направленную вниз (вверх).
Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вниз и вверх.
Теорема (необходимое условие перегиба). Вторая производная дважды дифференцируемой функции 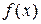 в точке перегиба
в точке перегиба 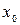 равна нулю, т.е.
равна нулю, т.е. 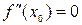 .
.
Теорема (достаточное условие перегиба). Если вторая производная 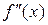 дважды дифференцируемой функции
дважды дифференцируемой функции 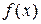 при переходе через некоторую точку
при переходе через некоторую точку 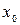 меняет свой знак, то
меняет свой знак, то 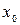 есть точка перегиба ее графика.
есть точка перегиба ее графика.
Алгоритм нахождения выпуклостей функции и точек перегиба:
1. Находим вторую производную 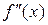 .
.
2. Находим точки, в которых 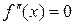 или не существует.
или не существует.
3. Исследуем знак 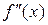 слева и справа от найденных точек и делаем вывод об интервалах выпуклости и о наличии точек перегиба.
слева и справа от найденных точек и делаем вывод об интервалах выпуклости и о наличии точек перегиба.
4. Находим значение функции в точках перегиба.
Пример. Найти точки перегиба графика функции 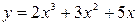 .
.
 2015-03-20
2015-03-20 2894
2894
