Решением неравенств с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.
Пример. Решим неравенство 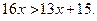
Перенесём слагаемое 13х с противоположным знаком в левую часть неравенства: 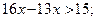
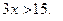
Разделим обе части неравенства на 3: 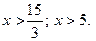
Множество решений неравенства состоит из всех чисел, больших 5.
Ответ: 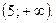


1.Решите неравенство:
1) 5х > 35; 2) 6х > 48; 3) 8х < 72; 4) 7х < 42;
а) 6 х ³ – 18; а) 5 х > – 45; а) 7 х £ – 14; а) 4 х < – 36;
б) – 4 х > 36; б) – 6 х ³ 42; б) – 9 х > 54; б) – 7 х £ 63;
5) -9х > -63; 6) -х > -8; 7) -х 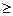 10; 8) -12х
10; 8) -12х 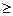 24;
24;
9) 3х > 11 10) 6х > 13 11) 6х 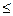 1,2 12) 4х
1,2 12) 4х 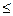 1,6
1,6
13) -18х 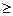 -27; 14) 12х
-27; 14) 12х 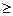 -18; 15) -15х
-18; 15) -15х 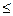 25; 16) -х
25; 16) -х 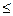 24;
24;
17) 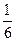 х > 3; 18)
х > 3; 18) 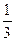 х > 2; 19) -
х > 2; 19) - 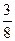 х < -12; 20) -
х < -12; 20) - 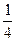 х < 6;
х < 6;
21) 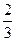 х > 18; 22)
х > 18; 22) 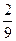 х > 36; 23) -
х > 36; 23) - 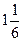 х < 42; 24) -
х < 42; 24) - 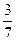 х < 21;
х < 21;
25) 0,4х > 2; 26) 0,5х > 3; 27) -0,3х < -9; 28) -0,7х < 1,4;
2. Решите неравенство:
1) 12 + х > 18; 2) 17 + х > 37; 3) 6 - х 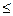 4; 4) 5 - х
4; 4) 5 - х 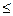 1;
1;
5) 6,2 + х 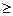 10; 6) 0,3 + х
10; 6) 0,3 + х 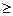 1; 7) 0,4 - х < 0; 8) 0,6 - 2х
1; 7) 0,4 - х < 0; 8) 0,6 - 2х 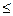 0;
0;
9) 1 + 3х > 10; 10) 1 + 6х > 7; 11) 6 - 5х 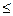 2; 12) 3 - 2х
2; 12) 3 - 2х 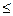 8;
8;
13) 6 + х > 3 – 2х; 14) 4 + х > 1 – 2х; 15) 19 + 4х 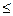 5х – 1;
5х – 1;
16) 7 + 4х 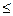 6х + 1; 17) 6х
6х + 1; 17) 6х 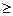 8х + 1; 18) 9х
8х + 1; 18) 9х 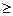 4х + 2;
4х + 2;
19) 3(2 + х) > 4 – х; 20) 4(1 + х) > х – 2;
21) – (4 – х) 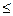 2(3 + х); 22) – (1 + 2 х)
2(3 + х); 22) – (1 + 2 х) 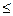 3(2 + х);
3(2 + х);
23) 0,5(х – 2) + 1,5 х < х + 1; 24) 1,2(х + 5) + 1,8 х > 7 + 2 х;
25) 1,5(х – 4) – 3,5 х < х + 6; 26) 2,4(5 – х) – 1,6 х > 2 х – 6;
27) 3(1 – х) + 2(2 – 2х) < 0; 28) 6(2х - 1) - 2(2 + х) < 0;
29) 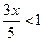 ; 30)
; 30) 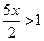 ; 31)
; 31) 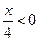 ; 32)
; 32) 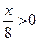 ;
;
33) 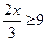 ; 34)
; 34) 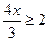 ; 35)
; 35) 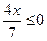 ; 36)
; 36) 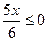 ;
;
37) 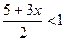 ; 38)
; 38) 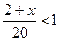 ; 39)
; 39) 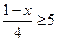 ; 40)
; 40) 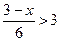 ;
;
41) 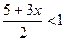 ; 42)
; 42) 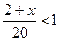 ; 43)
; 43) 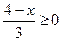 ; 44)
; 44) 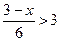 ;
;
45) 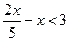 ; 46)
; 46) 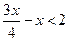 ; 47)
; 47) 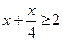 ; 48)
; 48) 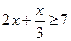 ;
;
49) 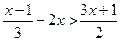 ; 50)
; 50) 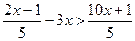 .
.
Тема 8. Решение систем неравенств с одной переменной.
 2015-04-08
2015-04-08 905
905








