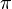2015-04-08
358
· 
— иррациональное число, то есть его значение не может быть точно выражено в виде дроби m/n, где m и n — целые числа. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. Иррациональность числа 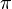была впервые доказанаИоганном Ламбертом в 1761 году[3] году путём разложения числа 
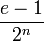в непрерывную дробь. В 1794 году Лежандр привёл более строгое доказательство иррациональности чисел 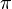и 
.
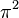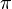· — трансцендентное число, то есть оно не может быть корнем какого-либо многочлена с целыми коэффициентами. Трансцендентность числа 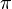была доказана в 1882 году профессором Кёнигсбергского, а позже Мюнхенского университетаЛиндеманом. Доказательство упростил Феликс Клейн в 1894 году.[4]
· Поскольку в евклидовой геометрии площадь круга и длина окружности являются функциями числа 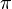, то доказательство трансцендентности 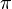положило конец спору о квадратуре круга, длившемуся более 2,5 тысяч лет.
· В 1934 году Гельфонд доказал трансцендентность числа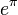 
.[5] В 1996 году Юрий Нестеренко доказал, что для любого натурального n числа 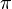и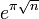 
алгебраически независимы, откуда, в частности, следует трансцендентность чисел 
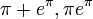и 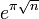.[6][7]
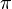· является элементом кольца периодов (а значит, вычислимым и арифметическим числом). Но неизвестно, принадлежит ли 
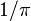к кольцу периодов.
