Геометрический период

То, что отношение длины окружности к диаметру одинаково для любой окружности, и то, что это отношение немногим более 3, было известно ещё древнеегипетским, вавилонским, древнеиндийским идревнегреческим геометрам. Самое раннее из известных приближений датируется 1900 годом до н. э.; это ²⁵/₈ (Вавилон) и ²⁵⁶/₈₁ (Египет), оба значения отличаются от истинного не более, чем на 1 %. Ведийский текст «Шатапатха-брахмана» даёт 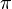как ³³⁹/₁₀₈ ≈ 3,139.

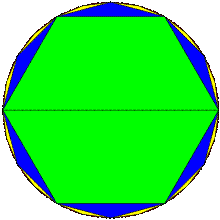
Алгоритм Лю Хуэя для вычисления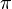

Архимед, возможно, первым предложил математический способ вычисления 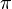. Для этого он вписывал в окружность и описывал около неё правильные многоугольники. Принимая диаметрокружности за единицу, Архимед рассматривалпериметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника как верхнюю оценку. Рассматривая правильный 96-угольник, Архимед получил оценку 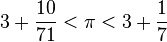и предположил, что 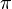примерно равняется 22/7 ≈ 3,142857142857143.

Чжан Хэн во II веке уточнил значение числа 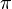, предложив два его эквивалента: 1) 92/29 ≈ 3,1724…; 2) 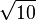≈ 3,1622.

В Индии Ариабхата и Бхаскара использовали приближение 3,1416.Варахамихира в 6 веке пользуется в «Панча-сиддхантике» приближением .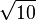

Около 265 года н. э. математик Лю Хуэй из царства Вэйпредоставил простой и точный итеративный алгоритм (англ. Liu Hui's π algorithm) для вычисления 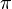с любой степенью точности. Он самостоятельно провёл вычисление для 3072-угольника и получил приближённое значение для 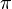по следующему принципу:

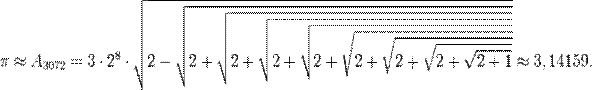
Позднее Лю Хуэй придумал быстрый метод вычисления 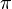и получил приближённое значение 3,1416 только лишь с 96-угольником, используя преимущества того факта, что разница в площади следующих друг за другом многоугольников формирует геометрическую прогрессию со знаменателем 4.

В 480-х годах китайский математик Цзу Чунчжи продемонстрировал, что 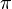≈ ³⁵⁵/₁₁₃, и показал, что 3,1415926 < 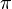< 3,1415927, используя алгоритм Лю Хуэя применительно к 12288-угольнику. Это значение оставалось самым точным приближением числа 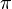в течение последующих 900 лет.