2015-04-12
1851
Рассмотрим колебательный контур, в котором активное сопротивление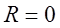 
и отсутствует внешнее сопротивление ЭДС (
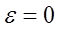). В данном случае (см. формулы 3,4) уравнение свободных незатухающих колебаний имеет вид
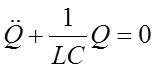(7)
Или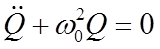 
, (7а)
Решение уравнения (7)
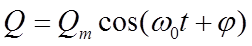(8)
Где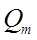 
- амплитуда колебаний заряда конденсатора; 
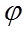- начальная фаза колебаний заряда на конденсаторе. Значения 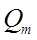, 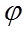определяются начальными условиями, а 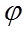- свойствами колебательного контура.
Период свободных незатухающих электрических колебаний определяется формулой Томсона:
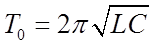(9)
Сила тока в колебательном контуре и напряжение в конденсаторе
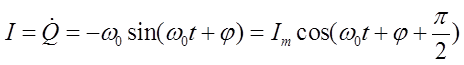(10)
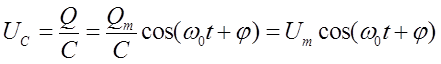(11)
Где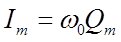 
, 
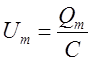- соответственно амплитуды силы тока и напряжения. Из выражений (8) и (10) вытекает, что колебания тока 
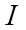опережают по фазе колебания заряда на 
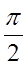, т.е. при достижении током максимального значения, заряд ((а также и напряжение (см.(11)) обращается в нуль, и наоборот.
