В интегралах 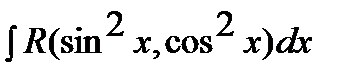 , где
, где 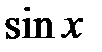 и
и 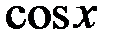 входят в подынтегральную рациональную функцию, только в четных степенях делается замена
входят в подынтегральную рациональную функцию, только в четных степенях делается замена 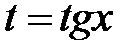 . При этом
. При этом
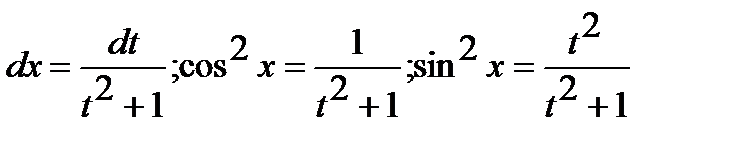 .
.
Этой же подстановкой к интегралам от рациональных функций приводятся интегралы вида 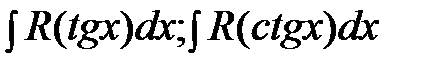 .
.
Пример: Найти неопределенный интеграл:
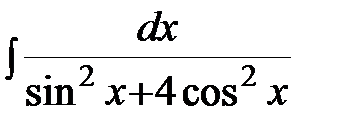 .
.
Решение: Сделаем подстановку:
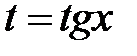 ;
; 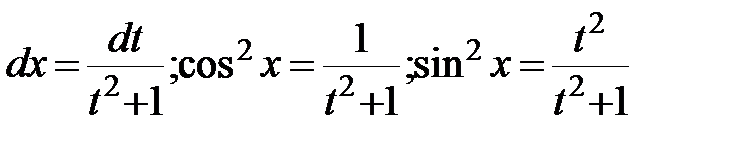 .
.
Тогда 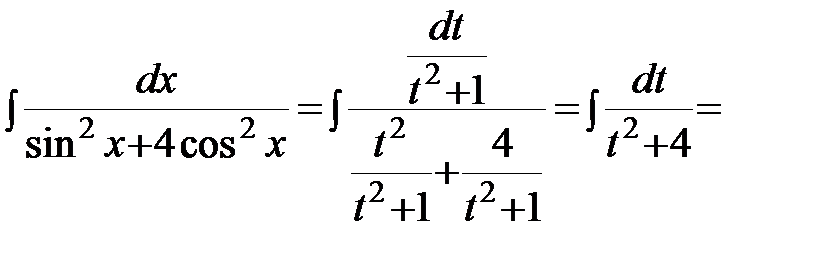
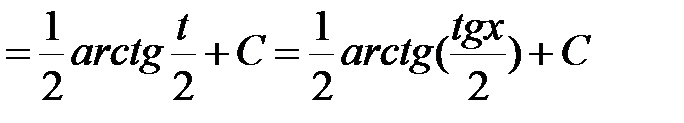 .
.
Пример. Найти неопределенный интеграл: 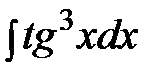 .
.
Решение: 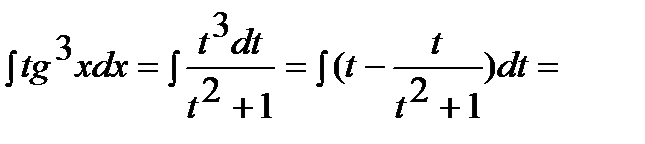

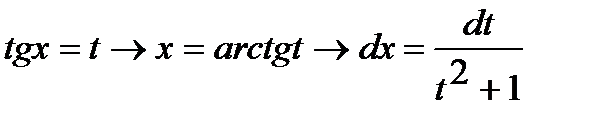
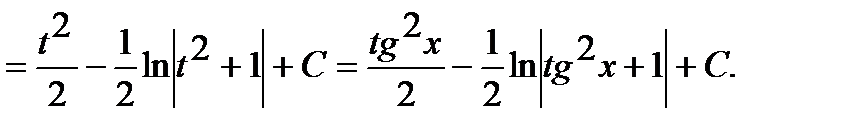
3-й случай. Интегрирование выражений вида
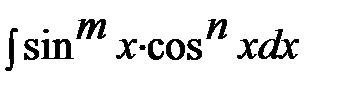 , (6)
, (6)
где m и n- целые числа. Рассмотрим два случая:
а) Среди чисел m,n есть хотя бы одно нечетное. Тогда за t принимается функция, стоящая в основании другой степени.
Пример. Найти неопределенный интеграл:
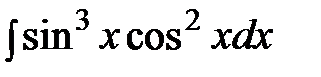 .
.
Решение: Здесь функция 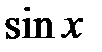 стоит в нечетной степени, поэтому
стоит в нечетной степени, поэтому 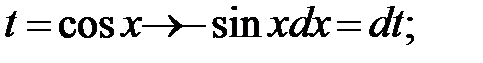
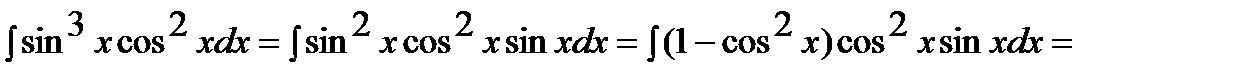
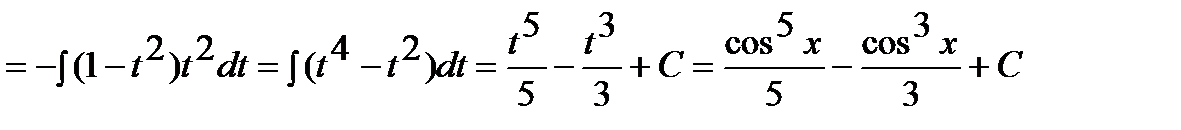 ;
;
б) В выражении (6) оба числа m,n - четные неотрицательные.
Положим m=2p, n=2q и применим формулы:
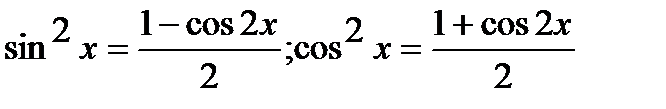 .
.
Тогда 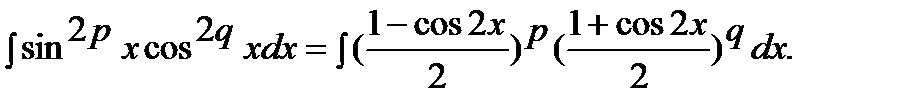
Раскрыв скобки, получим сумму интегралов, к каждому из которых применим 1-й или 2-й способы:
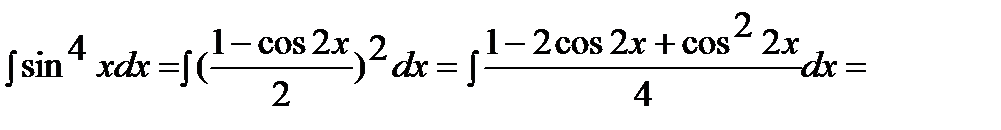
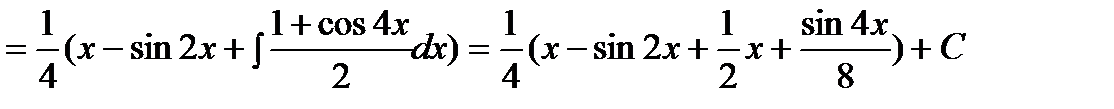 .
.
 2015-04-12
2015-04-12 396
396








