Пусть 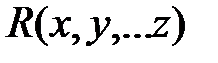 - рациональная функция своихаргументов. Тогда интеграл
- рациональная функция своихаргументов. Тогда интеграл 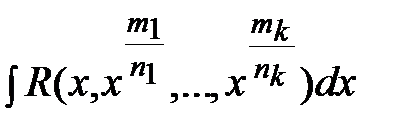 находится заменой переменных
находится заменой переменных 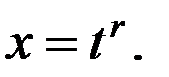
Как правило, за 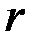 берется наименьшее общее кратное чисел
берется наименьшее общее кратное чисел 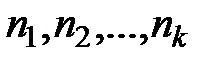 , где
, где 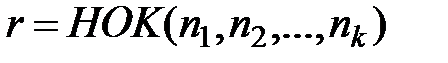 , т.е. r выбирается так, чтобы все корни, стоящие под знаком интеграла, извлекались.
, т.е. r выбирается так, чтобы все корни, стоящие под знаком интеграла, извлекались.
Пример 1. Вычислить неопределенный интеграл 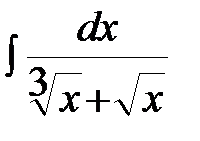 .
.
Решение:
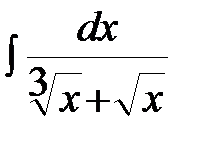
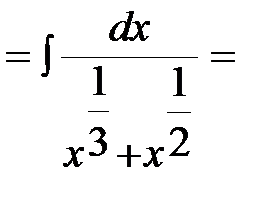
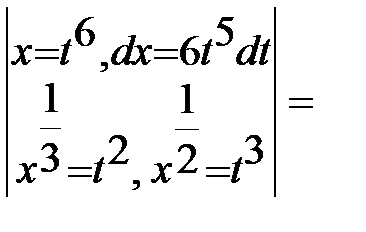
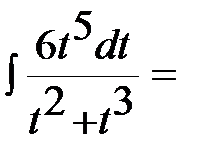
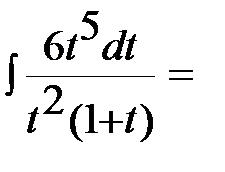
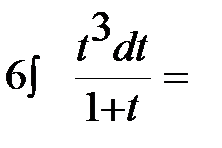
В подынтегральном выражении выделим целую часть: 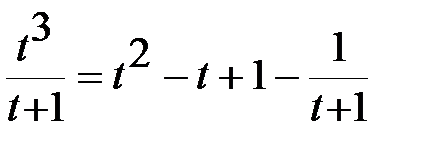 ,
,
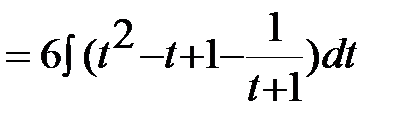
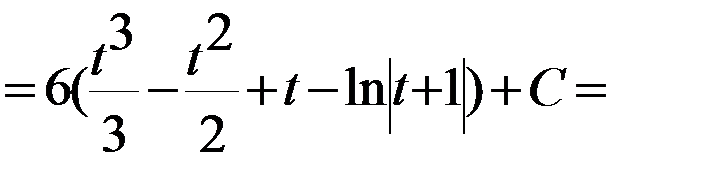
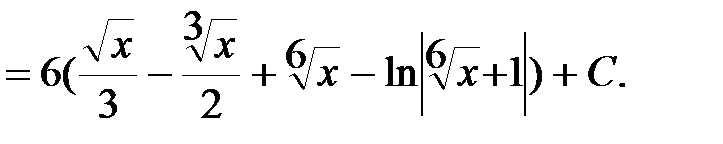
В некоторых случаях проинтегрировать иррациональные выражения помогают тригонометрические подстановки:
1) 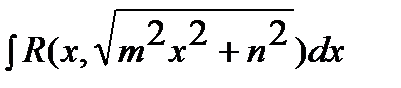 .
.
Такие выражения рационализируются с помощью следующей подстановки
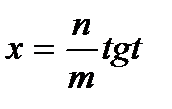 ,
, 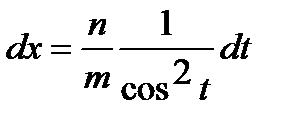 .
.
Пример 2. Найти неопределенный интеграл 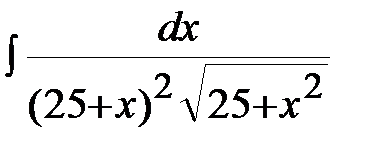 .
.
Замена 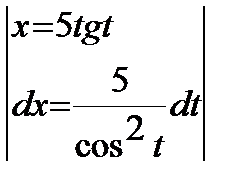 .
.
Интеграл примет вид: 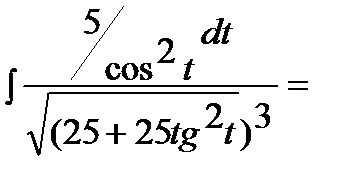
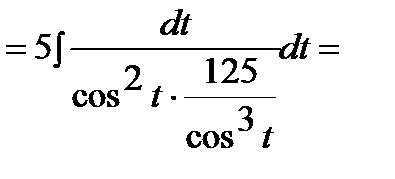
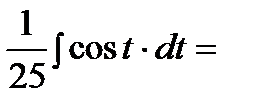
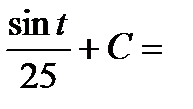
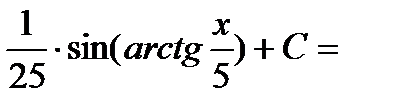
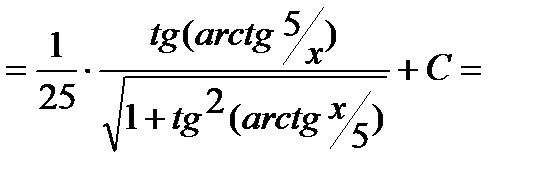
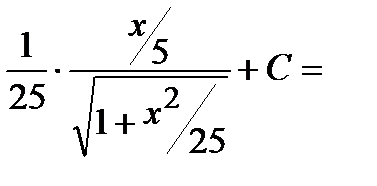
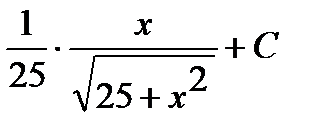 .
.
2) 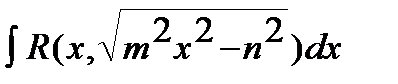
Такие выражения рационализируются с помощью следующей подстановки
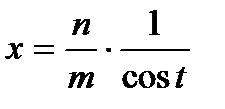 ,
, 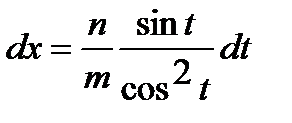 .
.
Пример 3. Найти неопределенный интеграл 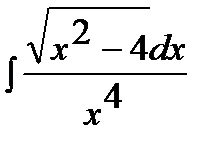 .
.
Замена 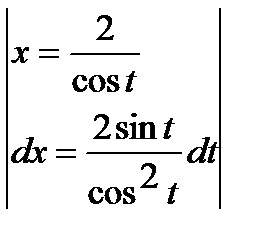 .
.
Тогда 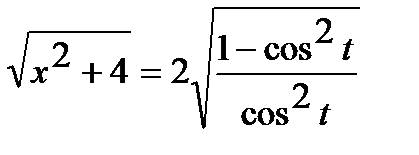
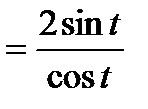 .
.
Интеграл примет вид: 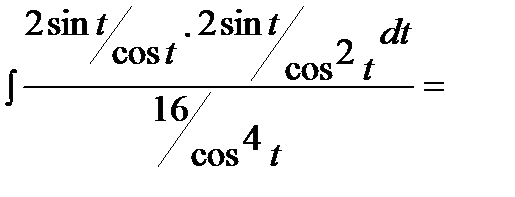
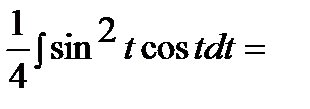
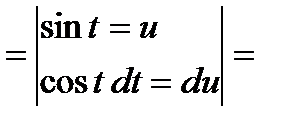
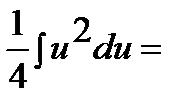
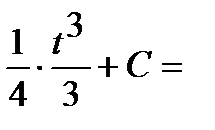
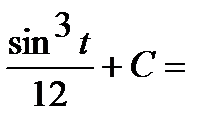
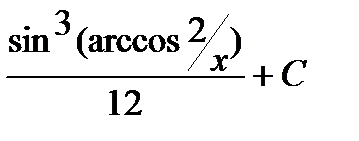
3) 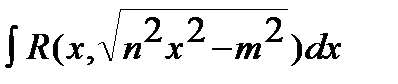 .
.
Такие выражения рационализируются с помощью следующей подстановки
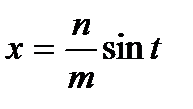 ,
, 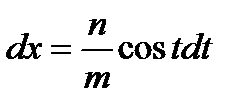 .
.
Пример 4. Найти неопределенный интеграл 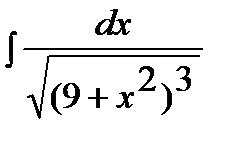 .
.
Замена 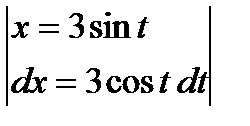 .
.
Тогда интеграл примет вид: 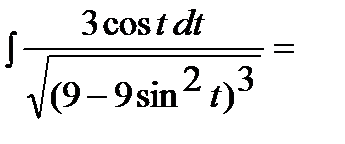
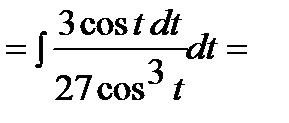
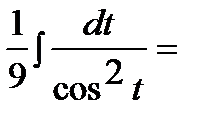
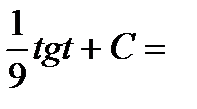
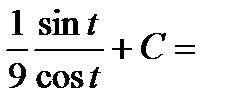
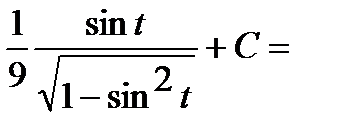
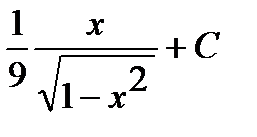 .
.
 2015-04-12
2015-04-12 810
810








