Определение: Если криволинейная трапеция ограничена линиями y=0; x=a; x=b; y=f(x), где f(x)³0 вращается вокруг оси OX, то полученное тело называется телом вращения вокруг оси OX.
Как известно, объем тела выражается через площадь поперечного сечения по формуле: 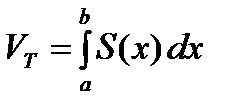 . В данном случае поперечными сечениями являются круги радиусом Rкр=f(x); Sкр=S(x) = pf2(x) ÞVOX =
. В данном случае поперечными сечениями являются круги радиусом Rкр=f(x); Sкр=S(x) = pf2(x) ÞVOX = 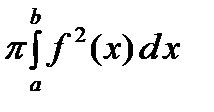 .
.
Если фигура, ограниченная кривыми y1=f1(x) и y2=f2(x) [0 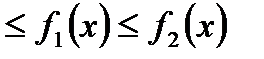 ] и прямыми x=a, x=b, вращается вокруг оси Ох, то объем тела вращения
] и прямыми x=a, x=b, вращается вокруг оси Ох, то объем тела вращения
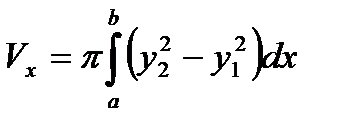

Если криволинейная трапеция ограниченная линиями 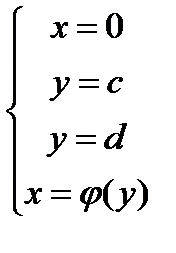 вращается вокруг оси OY, то объем полученного тела вращения V OY=
вращается вокруг оси OY, то объем полученного тела вращения V OY= 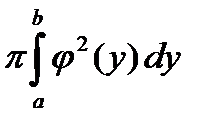 .
.
Пример: Вычислить объем тела вращения, ограниченного линиями y=0; x=0; x=1; y=ex.
| х |
| y |
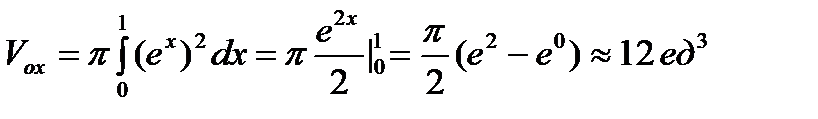
 2015-04-12
2015-04-12 667
667








