Предположим теперь, что функция 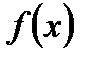 непрерывна на
непрерывна на 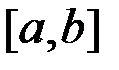 , за исключением точки
, за исключением точки 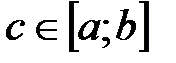 , в которой она терпит разрыв второго рода, и рассмотрим три случая:
, в которой она терпит разрыв второго рода, и рассмотрим три случая:
а) 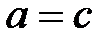 .
.
Возьмем произвольное, но достаточно малое (чтобы выполнялось неравенство 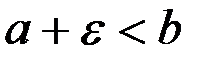 ) положительное
) положительное 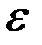 и положим, по определению,
и положим, по определению,  =
= 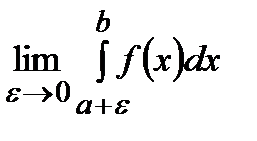 Если указанный предел существует, то
Если указанный предел существует, то 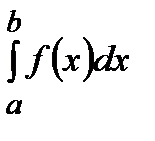 называется несобственным интегралом второго рода по промежутку
называется несобственным интегралом второго рода по промежутку 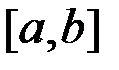 .
.
б) 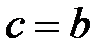 .
.
Как и в предыдущем случае определим несобственный интеграл 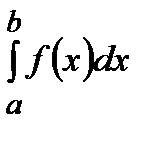 , положив:
, положив:
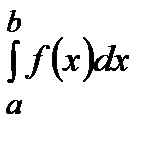 =
= 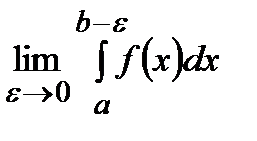 .
.
Отметим, что вся терминология, связанная с определением сходимости и расходимости несобственных интегралов второго рода полностью переносится с соответствующих определений, данных для интегралов первого рода.
в) 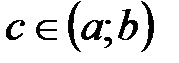
В этом случае полагаем:
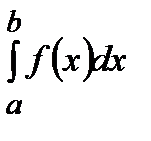 =
= 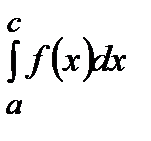 +
+ 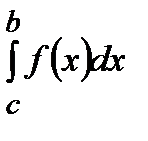
При этом будем считать, что последний несобственный интеграл сходится, если сходятся слагаемые, определяющие этот интеграл. Ясно, что,
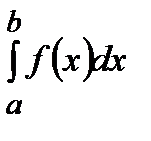 =
= 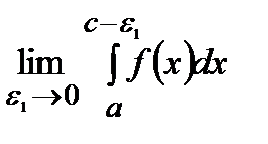 +
+ 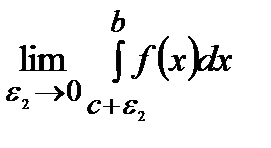 .
.
Пример.
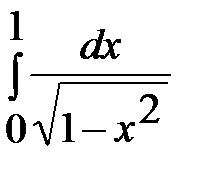 =
= 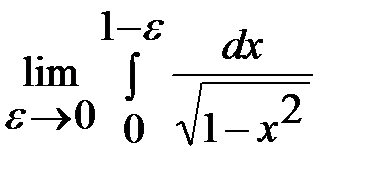 =
= 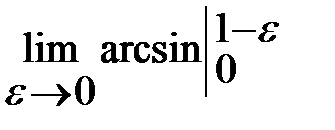 =
= 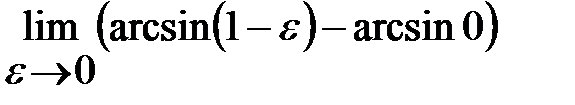 =
=
= 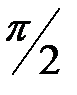
 2015-04-12
2015-04-12 309
309








