Для применения этого метода приведем систему (4.1) к виду:
| x 1 = (a 1,n+1- a 11 x 1- a 12 x 2-...- a 1n x n) / a 11+ x 1 | |
| x 2 = (a 2,n+1- a 21 x 1- a 22 x 2-...- a 2n x n) / a 22+ x 2 | (4.20) |
| ........................ | |
| x n = (a n,n+1- a n1 x 1- a n2 x 2-...- a nn x n) / a nn+ x n |
Зададимся некоторым начальным приближением 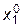 ,
, 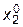 ,...,
,..., 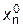 и подставим его значения в правые части (4.20), и получим новое приближение
и подставим его значения в правые части (4.20), и получим новое приближение 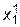 ,
, 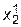 ,...,
,..., 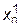 , которое подставим снова в систему (4.20) и т.д.
, которое подставим снова в систему (4.20) и т.д.
Таким образом организуется итерационный процесс, называемый методом простых итераций для систем алгебраических уравнений и являющийся обобщением метода простых итераций для алгебраических уравнений, рассмотренного в разделе 3:
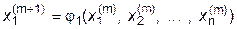
| |
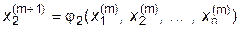
| (4.21) |
| ................................ | |
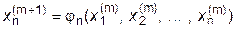
| , |
где 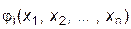 =(a i,n+1- a i1 x 1- a i2 x 2-...- a in x n) / a ii+ x i , i=1,2,...,n;
=(a i,n+1- a i1 x 1- a i2 x 2-...- a in x n) / a ii+ x i , i=1,2,...,n;
m - номер итерации.
Процесс (4.21) можно представить в несколько ином виде:
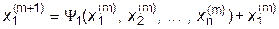
| |
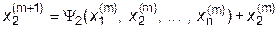
| (4.22) |
| ...................................... | |
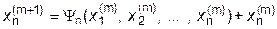
| , |
где 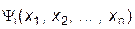 =(a i,n+1- a i1 x 1- a i2 x 2-...- a in x n) / a ii , i=1,2,...,n;
=(a i,n+1- a i1 x 1- a i2 x 2-...- a in x n) / a ii , i=1,2,...,n;
Значения 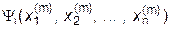 или короче
или короче 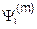 характеризуют разницу между m-м и (m+1)-м приближениями и образуют совокупность так называемых невязок (m+1)-го приближения.
характеризуют разницу между m-м и (m+1)-м приближениями и образуют совокупность так называемых невязок (m+1)-го приближения.
Процесс (4.21) или (4.22) является бесконечным вычислительным процессом, каждая новая итерация которого дает все лучшее приближение к точному решению системы. В качестве критерия окончания обычно берется выполнение условия: “Все невязки по абсолютной величине меньше наперед заданного числа 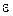 ”, характеризующего точность решения системы, т.е.
”, характеризующего точность решения системы, т.е.
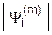 < < 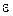 , i =1,2,...,n , i =1,2,...,n
| (4.23) |
Процесс (4.22) можно видоизменить, если использовать приближения к решениям, найденные в ходе текущей итерации, при проведении этой же итерации:
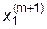
| = | 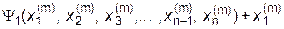
| |
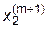
| = | 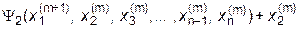
| |
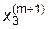
| = | 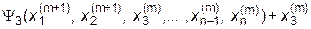
| (4.24) |
| ..... | . | ....................................... | |
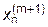
| = | 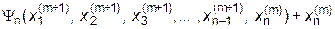
|
Этот процесс называется методом Зейделя. Он приводит, как правило, к ускорению сходимости по сравнению с процессом (4.22). Еще одним важным преимуществом метода Зейделя является меньший расход памяти ЭВМ, т.к. при его использовании необходим один массив для хранения вектора-столбца приближений, а в методе простых итераций - два: по массиву на предыдущее и текущее приближения.
Для сходимости итерационных методов, т.е. для выполнения условия (4.23) при некотором конечном m, необходимо, чтобы значения диагональных элементов матрицы СЛАУ были преобладающими по абсолютной величине по сравнению с другими элементами. Обеспечить это требование можно путем перестановки строк и (или) столбцов матрицы системы.
 2015-04-12
2015-04-12 442
442








