Отметим некоторые теоремы о пределах, которые часто применяются для решения задач.
Если существуют конечные пределы 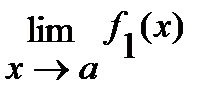 и
и 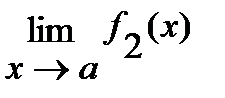 , то
, то
1) 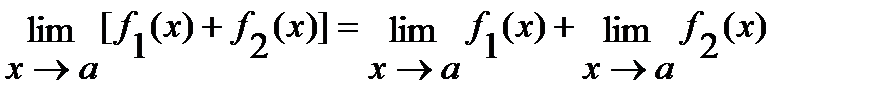 ;
;
2) 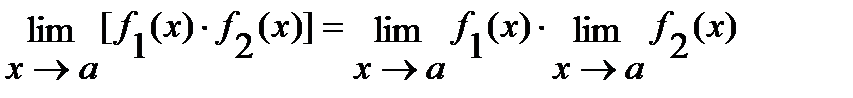 ;
;
3) 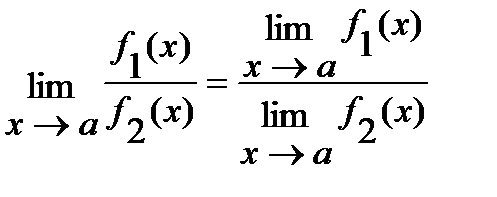 (если
(если 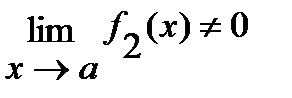 ).
).
Отметим еще два замечательных предела и следствия из них:
1) 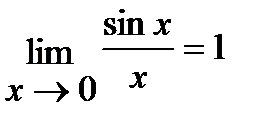 ;
;
2) 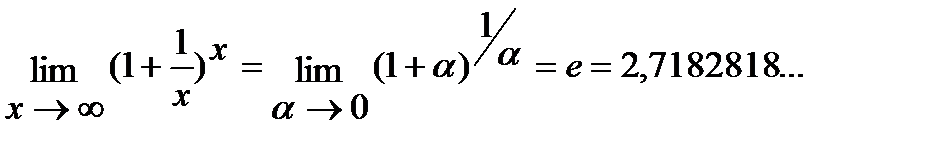 ;
;
3) 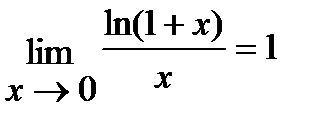 ; 4)
; 4) 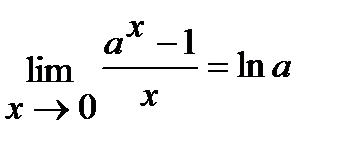 ; 5)
; 5) 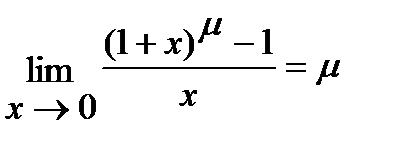 .
.
Задача. Найти указанные пределы, не пользуясь правилом Лопиталя:
а) 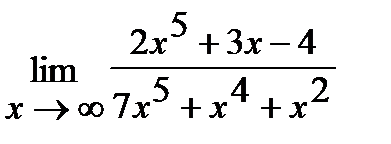 ;
;
б) 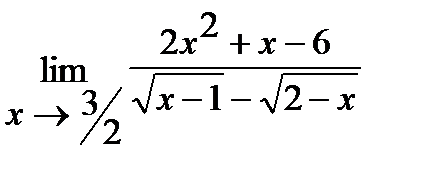 ;
;
в) 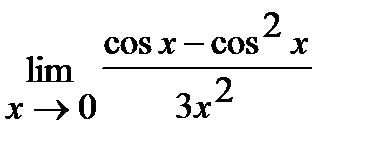 ;
;
г) 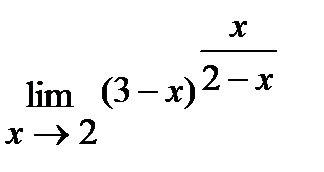 ;
;
д) 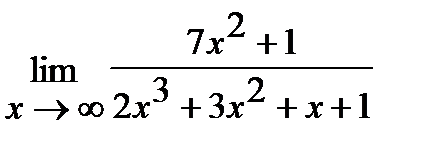 ;
;
е) 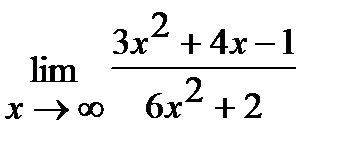 . ж)
. ж) 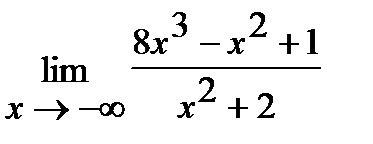 .
.
Решение. а) Если 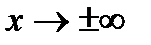 , то для нахождения предела частного двух многочленов достаточно разделить и числитель, и знаменатель дроби, стоящей под знаком предела, на
, то для нахождения предела частного двух многочленов достаточно разделить и числитель, и знаменатель дроби, стоящей под знаком предела, на 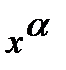 , где
, где 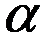 - степень многочлена, стоящего в знаменателе:
- степень многочлена, стоящего в знаменателе: 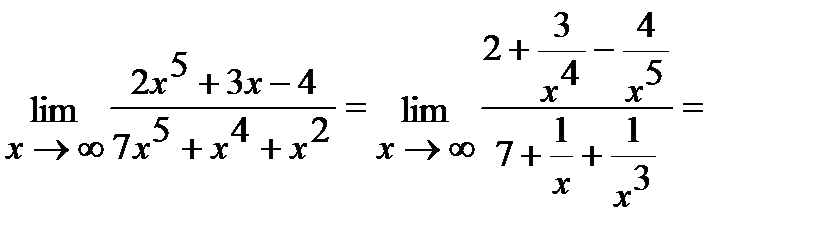
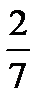 .
.
б) Умножим числитель и знаменатель дроби на 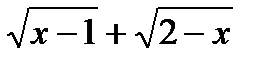 , избавившись тем самым от иррациональности в знаменателе. Итак,
, избавившись тем самым от иррациональности в знаменателе. Итак,
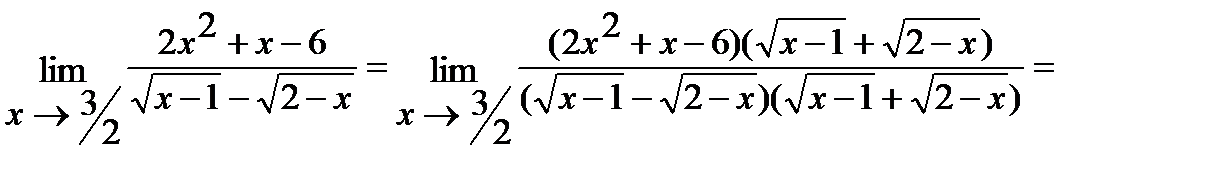
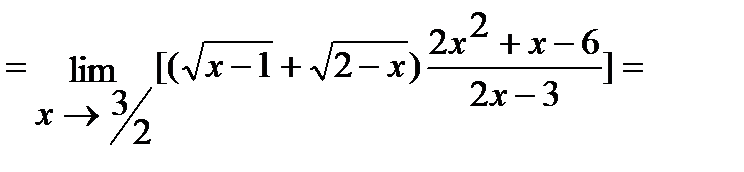
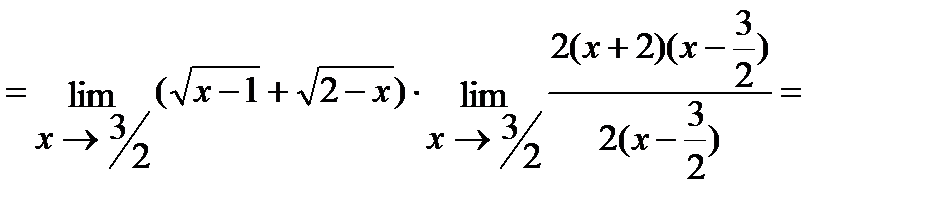
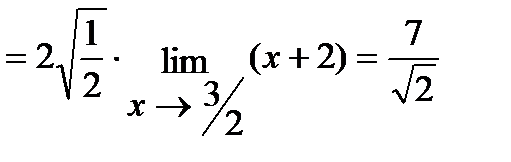 .
.
в) Для решения этой задачи воспользуемся первым замечательным пределом:
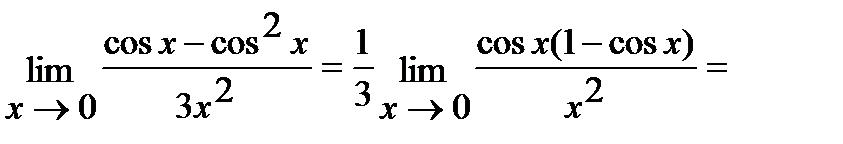
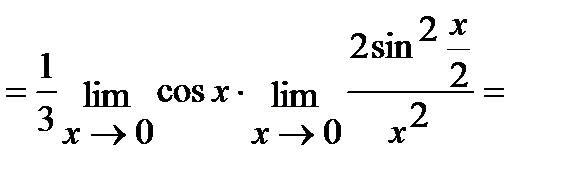
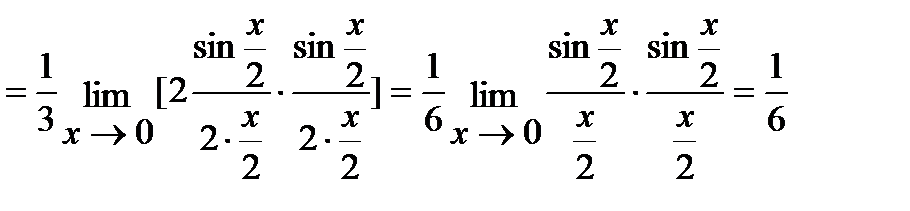
(Так как 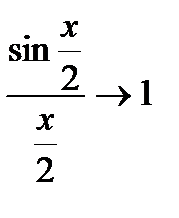 при
при 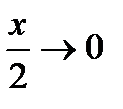 ).
).
г) Для решения данной задачи воспользуемся вторым замечательным пределом:
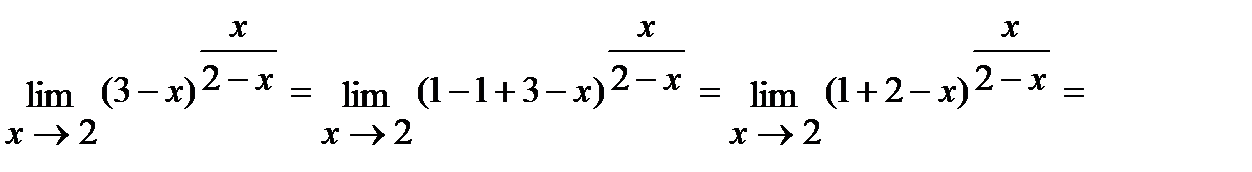
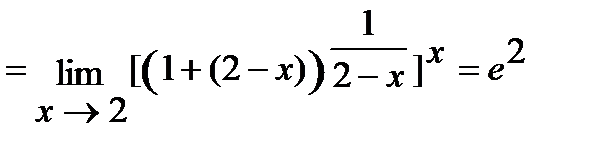 .
.
Последнее равенство вытекает из того, что в квадратной скобке стоит 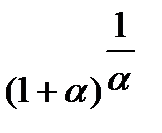 , где
, где 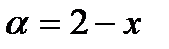 .
.
Решения задач е, ж аналогичны решению задачи а.
Например, задача ж имеет следующее решение:
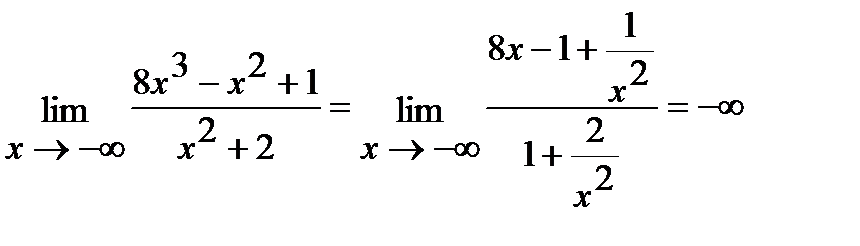 .
.
 2015-04-12
2015-04-12 499
499








