Нуль, и тогда, в силу теоремы из второго раздела, другой отличается от него на

числовой множитель. Запишем это: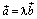

. Но эта же запись означает, что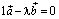

, и мы имеем нетривиальную линейную комбинацию, равную нулю.

Наоборот, допустим, что два неколлинеарных вектора

и 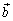линейно зависимы. Тогда

существуют коэффициенты λ и μ такие, что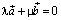

, причем, например, λ ≠ 0. Это означает, что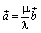

, и векторы коллинеарны, вопреки нашему предположению.

Следствие: Если два вектора неколлинеарны, то они линейно независимы.

Теорема: Любой вектор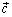

лежащий в одной плоскости с неколлинеарными векторами

и 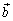, может быть представлен в

Виде линейной комбинации этих векторов (т.е. найдутся такие вещественные числа

λ и μ, что 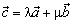). Такое