2015-04-12
266
Заметим, прежде всего, что оба вектора 
и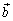 
отличны от нуля, так как если
бы хоть один из них был нулевым, то они были бы коллинеарны. Если вектор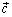 
Коллинеарен одному из данных векторов, то утверждение сводится к теореме из
Второго раздела.
В общем случае перенесем все три вектора в одну точку О (рис. 6). Через
конец C вектора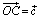 
проведем прямые CР и CQ, параллельные векторам
и 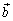. Тогда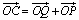 
, причем векторы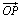 
и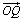 
коллинеарны соответственно и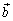
В силу теоремы из второго раздела существуют и определены однозначно такие
числа λ и μ, что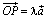 
, 
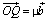
. Таким образом,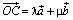 
, что и
