Следствие: Необходимым и достаточным условием линейной зависимости трех

векторов является их компланарность.

В самом деле, пусть векторы ,

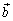
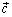, линейно зависимы, тогда один

из них есть линейная комбинация двух других. Пусть, например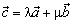

. Приложим векторы ,

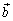
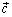, к одной и той же точке О

(рис. 7), так что ,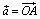

, .

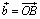
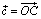Предположим сначала, что векторы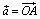

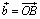, не коллинеарны; тогда несущие

их прямые определяют некоторую плоскость. В этой плоскости лежат и векторы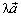

и 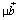, а значит, и весь

параллелограмм, на этих векторах построенный, в частности и его диагональ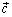

. Значит все три вектора ,

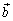
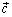, компланарны.

Если векторы и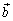

коллинеарны, то коллинеарны как векторы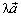

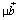, , так и их сумма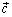

- три вектора ,

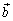
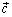, оказываются даже