левой)

Определение: Векторным произведением вектора

на вектор 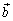называется вектор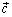

, удовлетворяющий условиям:

1. где φ – угол между векторами и ;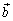

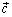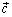2. вектор ортогонален вектору , вектор ортогонален вектору ;

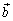3. упорядоченная тройка векторов 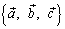является правой.

Если один из векторов нулевой, то векторное произведение есть нулевой вектор.

Векторное произведение вектора на вектор 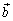обозначается 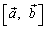{либо }.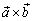

Теорема: Необходимым и достаточным условием коллинеарности двух векторов

Является равенство нулю их векторного произведения.