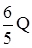Решение. Для перехода в делимом и делителе к целым коэффициентам умножим делимое на 6, что приведет к умножению на 6 искомого частного Q и остатка R

Для перехода в делимом и делителе к целым коэффициентам умножим делимое на 6, что приведет к умножению на 6 искомого частного Q и остатка R. После чего, умножим делитель на 5, что приведет к умножению частного 6Q и остатка 6R на 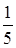. В итоге, частное и остаток, полученные при делении многочленов с целыми коэффициентами, в 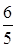раз будут отличаться от искомых значений частного Q и остатка R, полученных при делении данных многочленов.

12у⁴ ± 18ху³ 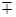30х²у² 6у² – 2ху – 9х² =

– 4ху³ – 12х²у² – 11х³у + 3х⁴

± 4ху³ 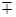6х²у² ± 10х³у

– 18х²у² – х³у + 3х⁴

± 18х²у² 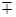27х³у ± 45х⁴

– 28х³у + 48х⁴ =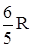

Следовательно, ;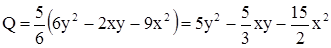

.

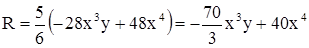Ответ: , .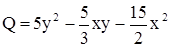

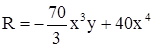Заметим, что если наибольший общий делитель данных многочленов найден, то, умножая его на любое число, не равное нулю, мы также получим наибольший делитель этих многочленов. Это обстоятельство дает возможность упрощать вычисления в алгоритме Евклида. А именно, перед очередным делением делимое или делитель можно умножать на числа, подобранные специальным образом так, чтобы коэффициент первого слагаемого в частном был числом целым. Как показано выше, умножение делимого и делителя приведет к соответствующему изменению частного остатка, но такому, что в итоге НОД данных многочленов умножится на некоторое равное нулю число, что допустимо.