Пусть M —множество элементов произвольной природы, для которых определены операции сложения и умножения на действительное число:
· паре элементов множества 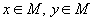 отвечает элемент
отвечает элемент 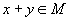 , называемый суммой x и y;
, называемый суммой x и y;
· паре 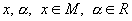 ,
, 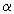 — любое действительное число, отвечает элемент
— любое действительное число, отвечает элемент 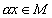 , называемый произведением числа
, называемый произведением числа 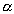 и элемента x.
и элемента x.
Будем называть множество M линейным пространством, если для всех его элементов определены операции сложения и умножения на действительное число и для любых элементов 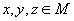 и произвольных чисел
и произвольных чисел 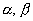 справедливо:
справедливо:
1. 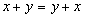 , сложение коммутативно;
, сложение коммутативно;
2. 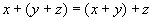 ,сложение ассоциативно;
,сложение ассоциативно;
3. существует единственный нулевой элемент 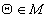 такой, что
такой, что 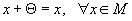 ;
;
4. для каждого элемента существует единственный противоположный элемент - x такой, что 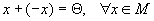 ,
,
5. 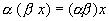 , умножение на число ассоциативно;
, умножение на число ассоциативно;
6. 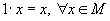 ;
;
7. 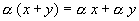 , умножение на число дистрибутивно относительно сложения элементов;
, умножение на число дистрибутивно относительно сложения элементов;
8. 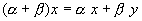 , умножение вектора на число дистрибутивно относительно сложения чисел.
, умножение вектора на число дистрибутивно относительно сложения чисел.
Равенства 1—8 называют аксиомами линейного пространства.
Линейное пространство часто называют векторным пространством, а его элементы — векторами.
Пример 1. Пространство 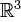 упорядоченных троек вещественных чисел
упорядоченных троек вещественных чисел 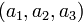 с операциями, определяемыми равенствами:
с операциями, определяемыми равенствами:
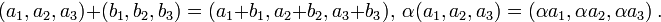
Геометрическая интерпретация очевидна: вектор в пространстве, «привязанный» к началу координат, может быть задан координатами своего конца 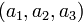 . На рисунке показано и типичное подпространство пространства
. На рисунке показано и типичное подпространство пространства 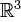 : плоскость, проходящая через начало координат.
: плоскость, проходящая через начало координат. 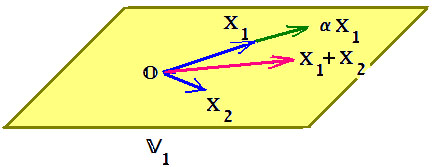 Точнее говоря, элементами
Точнее говоря, элементами 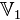 являются векторы, имеющие начало в начале координат и концы — в точках плоскости. Замкнутость такого множества относительно сложения векторов и их растяжения2) очевидна.
являются векторы, имеющие начало в начале координат и концы — в точках плоскости. Замкнутость такого множества относительно сложения векторов и их растяжения2) очевидна.
§
Исходя из этой геометрической интерпретации, часто говорят о векторе 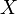 произвольного линейного пространства
произвольного линейного пространства 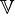 как о точке пространства
как о точке пространства 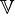 . Иногда эту точку называют «концом вектора
. Иногда эту точку называют «концом вектора 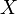 ». Кроме удобства ассоциативного восприятия, этим словам не придается никакого формального смысла: понятие «конец вектора» отсутствует в аксиоматике линейного пространства.
». Кроме удобства ассоциативного восприятия, этим словам не придается никакого формального смысла: понятие «конец вектора» отсутствует в аксиоматике линейного пространства.
П
Пример 2. Основываясь на том же примере, можно дать и иную интерпретацию векторного пространства 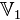 (заложенную, кстати, уже в самом происхождении слова «вектор»3)) — оно определяет набор «сдвигов» точек пространства
(заложенную, кстати, уже в самом происхождении слова «вектор»3)) — оно определяет набор «сдвигов» точек пространства 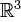 . Эти сдвиги — или параллельные переносы любой пространственной фигуры — выбираются параллельными плоскости
. Эти сдвиги — или параллельные переносы любой пространственной фигуры — выбираются параллельными плоскости 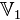 .
.
§
Вообще говоря, с подобными интерпретациями понятия вектора все обстоит не так просто. Попытки аппелировать к его физическому смыслу — как к объекту, имеющему величину и направление — вызывают справедливую отповедь строгих математиков. Определение же вектора как элемента векторного пространства очень напоминает эпизод с сепульками из знаменитого фантастического рассказа Станислава Лема (см. ☞ ЗДЕСЬ). Не будем зацикливаться на формализме, а исследуем этот нечеткий объект в его частных проявлениях.
П
Пример 3. Естественным обобщением 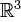 служит пространство
служит пространство 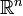 : векторное пространство строк
: векторное пространство строк 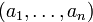 или столбцов
или столбцов 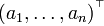 . Один из способов задания подпространства в
. Один из способов задания подпространства в 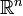 — задание набора ограничений. Множество решений системы линейных однородных уравнений:
— задание набора ограничений. Множество решений системы линейных однородных уравнений:
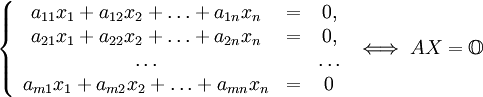
образует линейное подпространство пространства 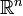 . В самом деле, если
. В самом деле, если
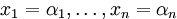
— решение системы, то и
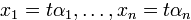
— тоже решение при любом 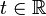 . Если
. Если
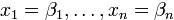
— еще одно решение системы, то и
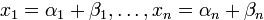
— тоже будет ее решением.
 2015-04-12
2015-04-12 1582
1582
