Опр 1. Система векторов 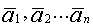 называется линейно зависимой, если сущ. числа
называется линейно зависимой, если сущ. числа 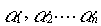 не все равные 0, такие что
не все равные 0, такие что 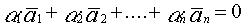 (1)
(1)
Система векторов 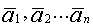 называется линейно независимой, если равенство (1) возможно только в том случае, когда все числа
называется линейно независимой, если равенство (1) возможно только в том случае, когда все числа 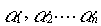 =0
=0
Выражение стоящее в левой части рав-ва (1) наз-ют линейной комбинацией векторов 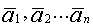
Опр 2. Система векторов является линейно зависимой, если существует линейная комбинация этих векторов с неравными 0 числами, которая тождественно равна.
Теор 1. Если система векторов 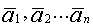 содержит нулевой вектор, то данная система линейно зависима.
содержит нулевой вектор, то данная система линейно зависима.
Док-во. Пусть 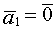 , тогда
, тогда 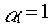
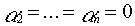
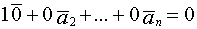
Теор 2. Если к системе линейно зависимых векторов 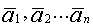 добавить произвольный вектор
добавить произвольный вектор 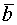 , то вновь полученная система будет линейно зависима.
, то вновь полученная система будет линейно зависима.
Док-во. Т.К. система векторов 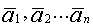 линейно зависима, то есть
линейно зависима, то есть 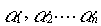 не все равные нулю, такие что
не все равные нулю, такие что 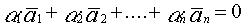 (2)
(2) 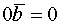 (3)
(3)
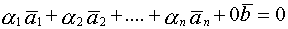 (4)
(4)
Есть 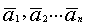 ,
, 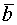
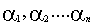 0 -не все равны нулю
0 -не все равны нулю
Следовательно система линейно зависима.
Следствие. Если к линейно зависимой системе добавить любое кол-во векторов, то полученная система будет линейно зависима.
Теор. (О линейной зависимости двух векторов.)
Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Док-во. 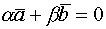
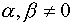
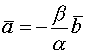
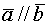 -коллинеарны
-коллинеарны
Теор. Три вектора линейно зависимы тогда и только тогда, когда они компланарны
Док-во. 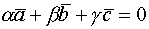
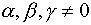
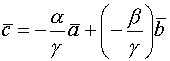
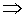
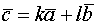
Для 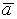 и
и 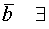 пл-ть
пл-ть 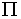 , что
, что 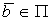 (или //) и
(или //) и 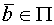
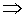
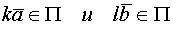
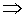
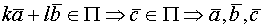 либо
либо 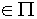 , либо // ей
, либо // ей  они компланарны.
они компланарны.
Теор. В трехмерном пространстве любые 4 вектора линейно зависимы.
Док-во.
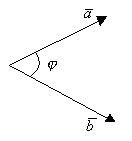
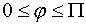
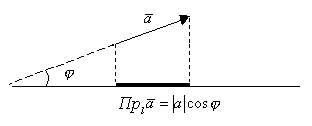
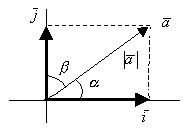
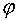 -угол между
-угол между 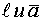
Вектор в системе координат
Базис-максимальная упорядоченная
система линейно независимых векторов.
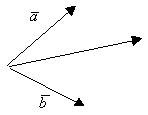
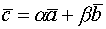
На плоскости 2 любых неколлинеарных вектора образуют базис.
ДПБ-базис, состоящий из ортогональных еденичных векторов.
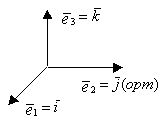
Операции над векторами в координатной форме.
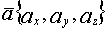
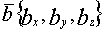
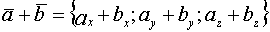
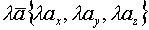
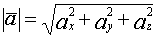
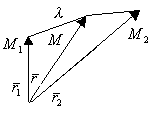
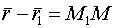
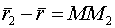
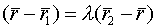
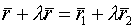
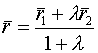
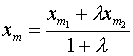
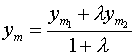
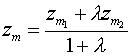
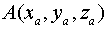 -нач.точка
-нач.точка 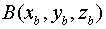 -кон.точка
-кон.точка
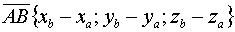

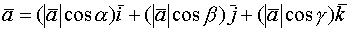
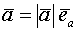
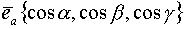
 2015-04-12
2015-04-12 6036
6036
