Группой 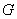 называется множество элементов, для которых определена некоторая операция
называется множество элементов, для которых определена некоторая операция 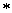 и выполняются следующие аксиомы:
и выполняются следующие аксиомы:
- G.1. Операция может быть применена к любым двум элементам группы, в результате чего получается третий элемент группы, т.е., если
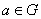 и
и 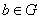 , то
, то 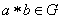 .
. - G.2. Для любых трех элементов
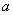 ,
, 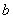 и
и 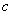 из
из 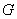
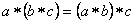 .
. - G.3. В
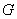 существует единичный элемент
существует единичный элемент 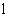 , т.е. такой, что
, т.е. такой, что 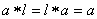 для любого
для любого 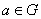 .
. - G.4. Для любого элемента
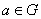 существует обратный элемент
существует обратный элемент 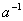 такой, что
такой, что 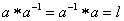 .
.
Аксиома G.1 определяет замкнутость операции в группе. Обычно операции над элементами записывают в виде 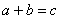 и называют сложением или в виде
и называют сложением или в виде 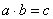 и называют умножением, даже если они не являются обычными сложением и умножением. В соответствии с двумя записями операций различают аддитивную и мультипликативную группы.
и называют умножением, даже если они не являются обычными сложением и умножением. В соответствии с двумя записями операций различают аддитивную и мультипликативную группы.
Свойство операции, сформулированное в виде аксиомы G.2, называют ассоциативностью. Она означает, что порядок выполнения операций несущественен, и поэтому скобки не нужны.
Аксиома G.3 постулирует обязательное существование единичного элемента. Для аддитивной группы единичный элемент называют нулем, обозначают 0 и определяют из уравнения 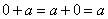 . Для мультипликативной группы единичный элемент называют единицей и определяют из уравнения
. Для мультипликативной группы единичный элемент называют единицей и определяют из уравнения 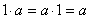 .
.
Аксиома G.4 требует для каждого элемента группы существования обратного элемента. Если групповая операция – сложение, то элемент, обратный 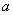 , обозначается
, обозначается  и находится из уравнения
и находится из уравнения 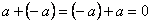 . Для мультипликативной группы обратный к
. Для мультипликативной группы обратный к 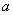 элемент обозначается
элемент обозначается 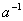 и находится из уравнения
и находится из уравнения 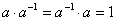 .
.
Группа называется коммутативной или абелевой, если кроме аксиом G.1 – G.5 выполняется следующая аксиома коммутативности.
G.5. Для двух произвольных элементов 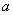 и
и 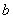 из
из 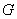 справедливо
справедливо 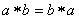 .
.
 2015-04-12
2015-04-12 378
378








