Простейшие свойства групп

Простейшие свойства

§ Обратный к данному элемент всегда определяется однозначно.

§ (a^-1)^{-1</sub> =} a^, aman ⁼ am⁺n^{, (}am⁾n ⁼ amn^.

§ (ab)^-1 = b^-1a^-1.

§ Верны законы сокращения:

c · a = c · b ⇔ a = b,

a · c = b · c ⇔ a = b.

§ Обратный элемент к нейтральному есть сам нейтральный элемент.

§ Группа содержит единственное решение x любого уравнения x · c = b или c · x = b; то есть в группе возможны однозначно определённые правое и левое «деление».

§ Пересечение двух подгрупп группы G есть подгруппа группы G.

§ Теорема Лагранжа: если G — группа конечного порядка g, то порядок g₁ любой её подгруппы G₁является делителем порядка группы. Из этого следует, что и порядок любого элемента делит порядок группы.

• В любой группе выполняется закон сокращения:

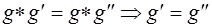(левый закон сокращения; аналогично, имеет место и правый закон)

Доказательство. Домножим равенство слева на 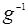и воспользуемся свойством ассоциативности:

.

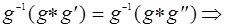
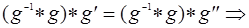
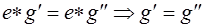• Признак нейтрального элемента:

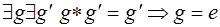
Доказательство Применим к равенству 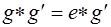закон сокращения.

• Признак обратного элемента:

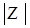
Доказательство: Применим закон сокращения к равенству

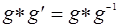
• Единственность обратного элемента. Обратный элемент определен однозначно. Следует из п.3.
• Существование обратной операции. Для любых двух элементов 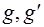произвольной группы G уравнение 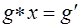имеет и притом единственное решение. Доказательство Непосредственно проверяется, что 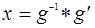(левое частное элементов 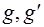) является решением указанного уравнения. Единственность вытекает из закона сокращения, примененного к равенству 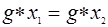. Аналогично устанавливается существование и единственность правого частного.