Говорят, что элемент (вектор) 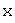 линейного пространства
линейного пространства 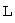 линейно выражается через элементы (векторы)
линейно выражается через элементы (векторы) 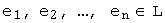 , если его можно представить в виде линейной комбинации этих элементов, т.е. представить в виде
, если его можно представить в виде линейной комбинации этих элементов, т.е. представить в виде 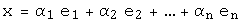 .
.
Если любой вектор системы  векторов линейного пространства
векторов линейного пространства 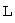 линейно выражается через остальные векторы системы, то система векторов называется линейно зависимой.
линейно выражается через остальные векторы системы, то система векторов называется линейно зависимой.
Система векторов, которая не является линейно зависимой, называется линейно независимой.
Справедливо следующее утверждение.
Система  векторов линейного пространства
векторов линейного пространства 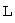 линейно независима тогда и только тогда, когда из равенства
линейно независима тогда и только тогда, когда из равенства 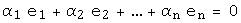 следует равенство нулю всех коэффициентов
следует равенство нулю всех коэффициентов 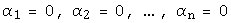 .
.
Если в линейном пространстве 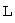 существует линейно независимая система из
существует линейно независимая система из 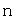 векторов, а любая система из
векторов, а любая система из 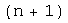 -го вектора линейно зависима, то число
-го вектора линейно зависима, то число 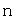 называется размерностью пространства
называется размерностью пространства 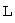 и обозначается
и обозначается 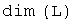 . В этом случае пространство
. В этом случае пространство 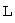 называют
называют 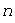 -мерным линейным пространством или
-мерным линейным пространством или 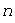 -мерным векторным пространством.
-мерным векторным пространством.
Любая упорядоченная линейно независимая система 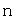 векторов
векторов 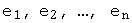 линейного пространства
линейного пространства 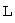 образует базис пространства и любой вектор
образует базис пространства и любой вектор 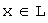 единственным образом выражается через векторы базиса:
единственным образом выражается через векторы базиса: 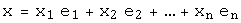 .
.
Числа 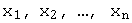 называют координатами вектора
называют координатами вектора 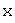 в базисе
в базисе 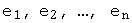 и обозначают
и обозначают 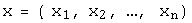 . При этом для любых двух произвольных векторов
. При этом для любых двух произвольных векторов 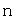 -мерного линейного пространства
-мерного линейного пространства 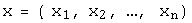 ,
, 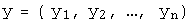 и произвольного числа
и произвольного числа 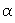 справедливо:
справедливо: 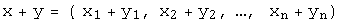 и
и 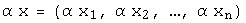 .
.
Это означает, что все 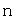 -мерные линейные пространства “устроены” одинаково -- как пространство
-мерные линейные пространства “устроены” одинаково -- как пространство 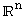 векторов-столбцов из
векторов-столбцов из 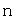 действительных чисел, т.е. что все они изоморфны пространству
действительных чисел, т.е. что все они изоморфны пространству 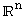 .
.
Линейные пространства 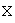 и
и 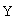 называются изоморфными, если между их элементами можно установить такое взаимно однозначное соответствие, что если векторам
называются изоморфными, если между их элементами можно установить такое взаимно однозначное соответствие, что если векторам 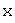 и
и 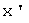 из
из 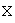 соответствуют векторы
соответствуют векторы 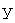 и
и 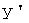 из
из 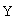 , то вектору
, то вектору 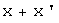 соответствует вектор
соответствует вектор 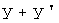 и при любом
и при любом 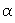 вектору
вектору 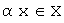 соответствует вектор
соответствует вектор 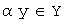 .
.
Изоморфизм 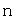 -мерных линейных пространств пространству
-мерных линейных пространств пространству 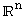 означает, что соотношения между элементами
означает, что соотношения между элементами 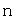 -мерного линейного пространства и операции с ними можно изучать как соотношения между векторами из
-мерного линейного пространства и операции с ними можно изучать как соотношения между векторами из 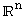 и операции с ними и что всякое утверждение относительно векторов из
и операции с ними и что всякое утверждение относительно векторов из 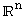 справедливо для соответствующих элементов любого
справедливо для соответствующих элементов любого 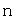 -мерного линейного пространства.
-мерного линейного пространства.
Например, доказано, что система векторов 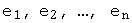 из
из 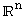
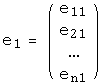 ,
, 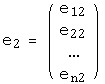 ,...,
,..., 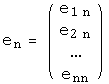
образует базис в 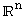 тогда и только тогда, когда отличен от нуля определитель матрицы, со столбцами
тогда и только тогда, когда отличен от нуля определитель матрицы, со столбцами 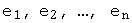 :
:

Для векторов 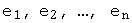 из
из 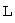 это означает, что они образуют базис в
это означает, что они образуют базис в 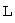 тогда и только тогда, когда отличен от нуля определитель матрицы, столбцами которой являются компоненты векторов
тогда и только тогда, когда отличен от нуля определитель матрицы, столбцами которой являются компоненты векторов 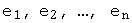 .
.
Пусть 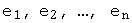 и
и 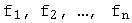 -- два базиса в
-- два базиса в 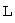 . Матрицей перехода от базиса
. Матрицей перехода от базиса 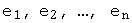 к базису
к базису 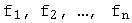 называется матрица
называется матрица  , столбцами которой являются координаты векторов
, столбцами которой являются координаты векторов 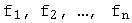 в базисе
в базисе 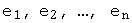 :
:
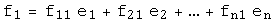 | 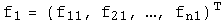 |
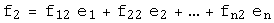 | 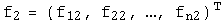 |
| ... | ... |
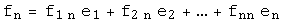 | 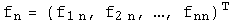 |
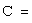
 ,
, 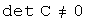
Вектор 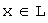 линейно выражается через векторы обоих базисов. Тогда, если
линейно выражается через векторы обоих базисов. Тогда, если 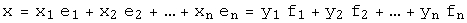 , то координаты вектора
, то координаты вектора 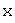 в базисе
в базисе 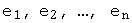 , и его координаты в базисе
, и его координаты в базисе 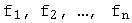 связаны соотношениями
связаны соотношениями

ПРИМЕР 1. Нахождение координат вектора в новом базисе.
 2015-04-12
2015-04-12 822
822








