Преимущества ортонормированного базиса

Для ортонормированного базиса 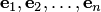формула (8.32) упрощается, так как из условия (8.31) следует, что матрица Грама 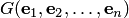ортонормированной системы 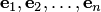равна единичной матрице: .

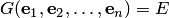1. В ортонормированном базисе 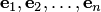скалярное произведение векторов 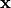и 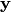находится по формул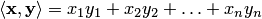е: , где 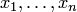— координаты вектор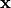а , а 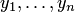— координаты вектора .

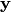2. В ортонормированном базисе 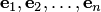длина вектора 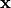вычисляется по формул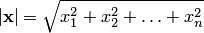е , где 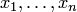— координаты вектора .

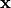3. Координаты 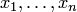вектора 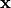относительно ортонормированного базиса 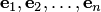находятся при помощи скалярного произведения по формулам:.

В самом деле, умножая обе части равенств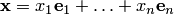а на 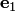, получаем

Аналогично доказываются остальные формулы.

Скалярное произведение векторов