Определение и примеры нормированных пространств

Нормированное пространство

Линейное пространство L называется нормированным, если любому его элементу x поставлено в соответствие число, называемое нормой и обозначаемое 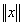, причем при этом выполнены следующие условия:

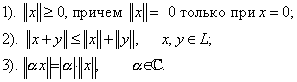
Всякое нормированное пространство становится метрическим, если ввести в нем расстояние 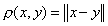. Справедливость аксиом метрического пространства вытекает из свойств 1) – 3) нормы. На нормированные пространства переносятся, таким образом, все понятия и факты, которые были изложены для метрических пространств.

Примеры.

6.3.1. Множество вещественных чисел становится нормированным пространством, если положить .

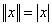6.3.2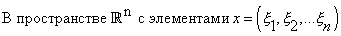

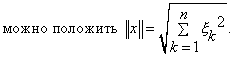
Заметим, что в этом же пространстве можно ввести норму и по-другому, например, так

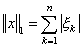или .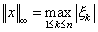

(Аксиомы нормы 1)-3) выполняются).

6.3.3. В пространстве 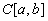непрерывных функций на отрезке 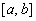определим норму формулой

.

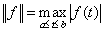Соответствующее расстояние уже рассматривалось в разделе 6.1. "Метрическое пространство" в примере 6.1.3.

.

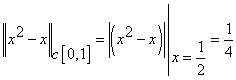Полное нормированное пространство называется банаховым пространством.