2015-04-12
3448
Ненулевой вектор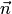 
, перпендикулярный заданной плоскости, называется нормальным вектором (или, короче, нормалью) для этой плоскости.
Пусть в координатном пространстве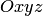 
(в прямоугольной системе координат) заданы:
а) точка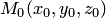 
;
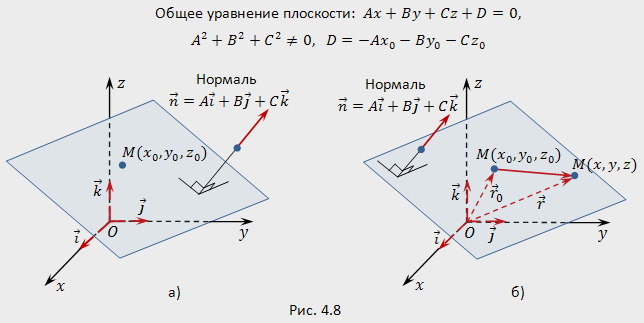
б) ненулевой вектор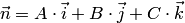 
(рис.4.8,а).
Требуется составить уравнение плоскости, проходящей через точку 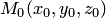перпендикулярно вектору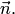 
Выберем в пространстве произвольную точку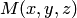 
. Обозначим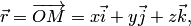 
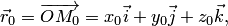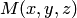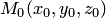— радиус-векторы точек и Точка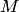 
принадлежит заданной плоскости тогда и только тогда, когда векторы 
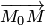и 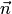перпендикулярны (рис.4.8,б). Условие ортогональности запишем при помощи скалярного произведения:
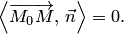
Учитывая, что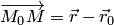 
, получаем векторное уравнение плоскости:
| (4.12) |
Это уравнение можно записать в другой форме. Преобразуем левую часть используя свойства скалярного произведения. Обозначая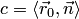 
получаем уравнение 
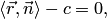или
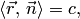
| (4.13) |
выражающее постоянство проекций на нормаль радиус-векторов точек, принадлежащих плоскости.
Получим координатную форму записи векторного уравнения плоскости (4.12). Так как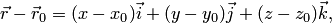 
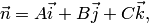формуле (1.10) находим
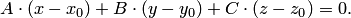
| (4.14) |
Полученное соотношение (4.14) позволяет по координатам точки 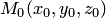и координатам 
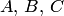нормали 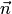сразу записать искомое уравнение плоскости.
Обозначив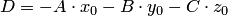 
, получим общее уравнение плоскости
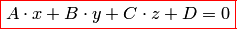
| (4.15) |
Поскольку коэффициенты 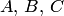не равны нулю одновременно (это координаты ненулевого вектора 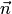), уравнение (4.15) является алгебраическим уравнением первой степени, т.е. линейным уравнением с тремя неизвестными. Следовательно, плоскость является алгебраической поверхностью первого порядка.
Проводя рассуждения в обратном порядке, делаем вывод о том, что линейное уравнение (4.15) задает в координатном пространстве плоскость. Полученные выводы сделаны для прямоугольной системы координат, но, учитывая теорему 4.1, они переносятся (без изменений) и на любую аффинную систему координат.
