Пусть заданы:
а) плоскость, описываемая общим уравнением (4.15): 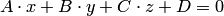 ;
;
б) точка 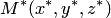 в пространстве.
в пространстве.
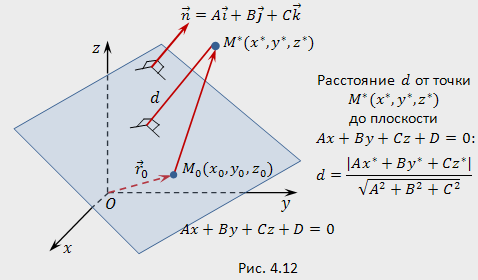
Требуется найти расстояние 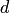 от точки до плоскости.
от точки до плоскости.
Искомое расстояние равняется длине ортогональной проекции вектора 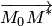 на направление нормали
на направление нормали 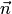 (рис.4.12) и находится по формуле:
(рис.4.12) и находится по формуле:
,
где 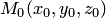 — любая точка на заданной плоскости.
— любая точка на заданной плоскости.
Запишем правую часть в координатной форме, выражая скалярное произведение и длину через координаты векторов
Поскольку координаты точки 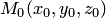 удовлетворяют уравнению (4.15), то
удовлетворяют уравнению (4.15), то 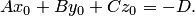 Подставляя это выражение, получаем формулу расстояния от точки до плоскости
Подставляя это выражение, получаем формулу расстояния от точки до плоскости
Пример 4.6. В координатном пространстве 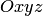 (в прямоугольной системе координат) заданы точки
(в прямоугольной системе координат) заданы точки 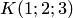 и
и 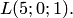 Требуется найти, в каком отношении плоскость
Требуется найти, в каком отношении плоскость 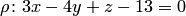 делит отрезок
делит отрезок 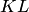 (рис.4.13).
(рис.4.13).
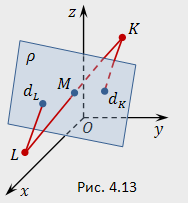
Решение. Найдем значения линейного четырехчлена 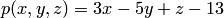 в точках
в точках 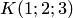 и
и 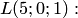
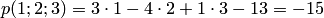 и
и 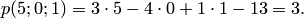
Получили значения разных знаков. Следовательно, точки 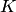 и
и 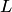 лежат по разные стороны от плоскости я (согласно пункту 4 замечаний 4.2, эти точки лежат в разных полупространствах), т.е. плоскость
лежат по разные стороны от плоскости я (согласно пункту 4 замечаний 4.2, эти точки лежат в разных полупространствах), т.е. плоскость 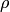 действительно пересекает отрезок
действительно пересекает отрезок 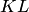 (в точке
(в точке 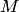 на рис.4.13). Так как эти значения по абсолютной величине пропорциональны расстояниям от точек
на рис.4.13). Так как эти значения по абсолютной величине пропорциональны расстояниям от точек 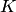 и
и 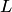 до плоскости
до плоскости 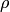 , то
, то
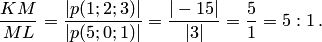
Этот же результат можно получить по формуле (4.16). Находим расстояния 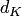 и
и 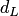 от точек
от точек 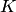 и
и 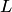 до плоскости
до плоскости 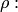
Следовательно, 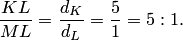
 2015-04-12
2015-04-12 1059
1059
