1. При составлении общего уравнения плоскости нормаль выбирается неоднозначно: можно выбрать любую, отличную от нуля, длину нормали 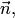 а также одно из двух возможных направлений (противоположный вектор
а также одно из двух возможных направлений (противоположный вектор 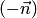 также является нормалью). Например, вместо нормали
также является нормалью). Например, вместо нормали 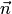 можно взять нормаль
можно взять нормаль 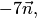 что соответствует умножению обеих частей уравнения (4.15) на число –7.
что соответствует умножению обеих частей уравнения (4.15) на число –7.
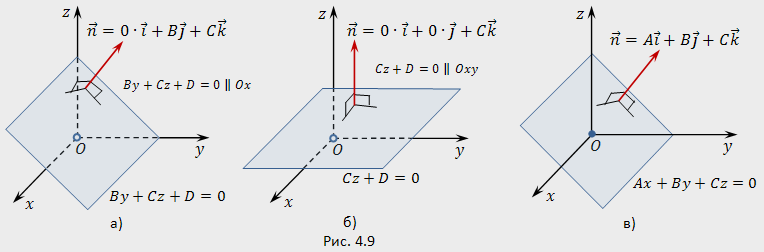
2. Если в общем уравнении плоскости (4.15) коэффициент при неизвестной равен нулю, то плоскость параллельна координатной оси. Например, если 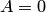 то плоскость (4.15) параллельна оси абсцисс
то плоскость (4.15) параллельна оси абсцисс 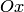 (рис.4.9,а); если
(рис.4.9,а); если 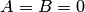 то плоскость (4.15) параллельна координатным осям
то плоскость (4.15) параллельна координатным осям 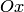 и
и 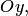 т.е. параллельна координатной плоскости
т.е. параллельна координатной плоскости 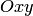 (рис.4.9,б).
(рис.4.9,б).
Если в общем уравнении плоскости (4.15) свободный член равен нулю 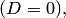 то плоскость проходит через начало координат (рис.4.9,в).
то плоскость проходит через начало координат (рис.4.9,в).
3. Нормаль 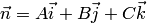 к плоскости
к плоскости 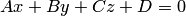 совпадает с градиентом функции
совпадает с градиентом функции 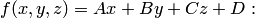
В курсе математического анализа доказывается, что градиент направлен в сторону наискорейшего возрастания функции в данной точке.
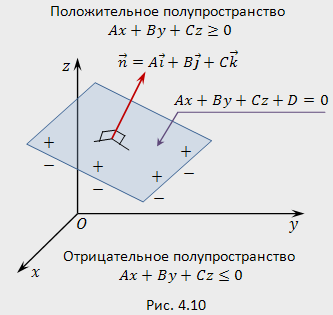
4. Плоскость 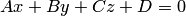 разбивает пространство на два полупространства (рис.4.10): положительное, координаты всех точек которого удовлетворяют неравенству
разбивает пространство на два полупространства (рис.4.10): положительное, координаты всех точек которого удовлетворяют неравенству 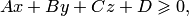 и отрицательное, для точек которого
и отрицательное, для точек которого 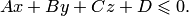 Нормаль
Нормаль 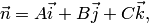 приложенная к произвольной точке плоскости
приложенная к произвольной точке плоскости 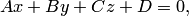 указывает на положительное полупространство (рис.4.10).
указывает на положительное полупространство (рис.4.10).
Это свойство следует из пункта 3.
5. Абсолютное значение 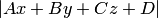 пропорционально расстоянию от точки
пропорционально расстоянию от точки 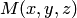 до плоскости
до плоскости 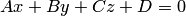 т.е. отношение расстояний от точек
т.е. отношение расстояний от точек 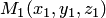 и
и 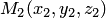 до плоскости
до плоскости 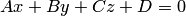 равно отношению
равно отношению 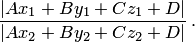
Доказательство аналогично доказательству пункта 5 замечаний 3.2.
6. В аффинной системе координат 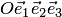 линейное уравнение
линейное уравнение 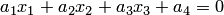 задает, согласно теореме 4.2, плоскость. Выводы, полученные в п.2,3,4,5, остаются справедливыми с тем лишь исключением, что вектор
задает, согласно теореме 4.2, плоскость. Выводы, полученные в п.2,3,4,5, остаются справедливыми с тем лишь исключением, что вектор 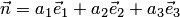 не является нормалью.
не является нормалью.
Пример 4.5. В координатном пространстве 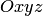 (в прямоугольной системе координат) заданы точки
(в прямоугольной системе координат) заданы точки 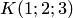 и
и 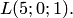 Составить уравнение плоскости, перпендикулярной отрезку
Составить уравнение плоскости, перпендикулярной отрезку 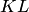 и проходящей через его середину (рис.4.11).
и проходящей через его середину (рис.4.11).
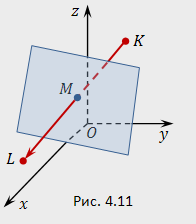
Решение. Находим координаты середины 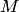 отрезка
отрезка 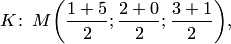 т.е.
т.е. 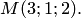 Вектор
Вектор 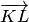 можно взять в качестве нормали к плоскости. Находим координаты этого вектора, вычитая из координат его конца соответствующие координаты его начала:
можно взять в качестве нормали к плоскости. Находим координаты этого вектора, вычитая из координат его конца соответствующие координаты его начала:
Следовательно, уравнение (4.15) искомой плоскости имеет вид 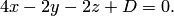
Осталось найти величину свободного члена 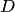 . Поскольку точка
. Поскольку точка 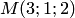 принадлежит плоскости, то ее координаты
принадлежит плоскости, то ее координаты 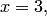
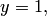
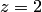 должны удовлетворять уравнению этой плоскости, следовательно,
должны удовлетворять уравнению этой плоскости, следовательно, 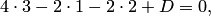 отсюда
отсюда 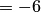 Таким образом, искомая плоскость задается уравнением
Таким образом, искомая плоскость задается уравнением

Уравнение этой прямой можно было получить в виде (4.14), подставляя координаты нормали 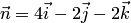 и точки
и точки 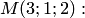
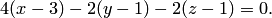
 2015-04-12
2015-04-12 443
443








