Параболой называется множество точек плоскости, равноудаленных от точки, называемой фокусом и прямой, называемой директрисой.
Уравнение параболы с вершиной в начале координат имеет вид:
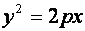 , (8)
, (8)
где 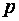 - расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты
- расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты 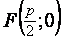 .
.
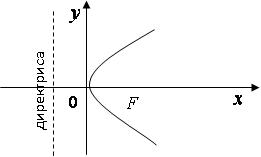
Рис. 5
Если вершина параболы находится в точке 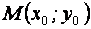 , то уравнение имеет вид:
, то уравнение имеет вид:
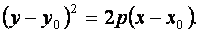 (9)
(9)
Задача 1. Составить уравнение геометрического места точек, равноотстоящего от оси Оу и точки 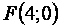 .
.
Решение: Возьмем на искомой линии произвольную точку 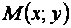 . Расстояние точки М от точки F определится по формуле расстояния между двумя точками:
. Расстояние точки М от точки F определится по формуле расстояния между двумя точками:
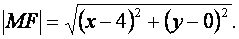
Расстояние точки М до оси Оу определится:
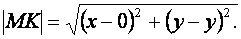
Так как по условию 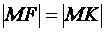 , то искомая кривая имеет уравнение:
, то искомая кривая имеет уравнение:
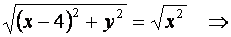
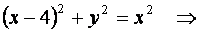
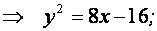
Линия, определяемая полученным уравнением 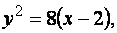 является параболой.
является параболой.
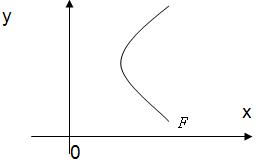
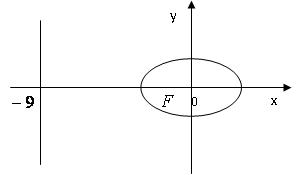
Задача 2. Составить уравнение геометрического места точек, отношение расстояний которых до точки F (-1; 0) и до прямой х = -9 равно 1/3.
Решение: Возьмём на искомой кривой произвольную точку 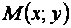 .
.
Её расстояния от точки 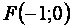 и прямой составляют
и прямой составляют 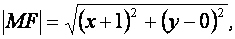
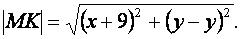
Из условия задачи следует:
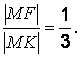
Таким образом, искомая кривая имеет уравнение:
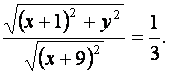
Приведём это уравнение к каноническому виду:
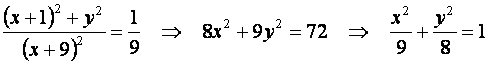 - это уравнение эллипса с полуосями:
- это уравнение эллипса с полуосями: 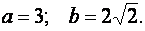
 2015-04-12
2015-04-12 1503
1503
