Если две плоскости 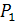 и
и 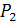 заданы общими уравнениями вида:
заданы общими уравнениями вида:
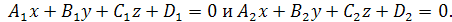
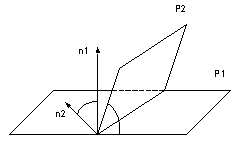 | Под углом между плоскостями 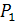 и и 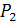 понимается один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между понимается один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между 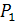 и и 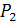 равен углу между их нормалями, то есть между векторами равен углу между их нормалями, то есть между векторами 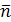 1 1 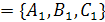 и и 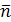 2 2 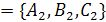 . Из формулы . Из формулы 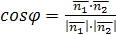 получаем, что косинус угла между плоскостями получаем, что косинус угла между плоскостями 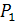 и и 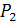 равен равен 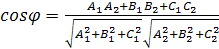 . . |
Условие параллельности плоскостей (рис.б) заключается в параллельности нормалей 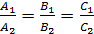 , а условие перпендикулярности плоскостей – в перпендикулярности нормалей или равенстве нулю их скалярного произведения:
, а условие перпендикулярности плоскостей – в перпендикулярности нормалей или равенстве нулю их скалярного произведения: 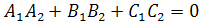 .
.

Для нахождения острого угла следует взять модуль правой части.
Если плоскости 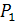 и
и 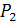 перпендикулярны, то таковы же их нормали,
перпендикулярны, то таковы же их нормали,
т. е. 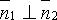 и наоборот.\
и наоборот.\
 2015-04-12
2015-04-12 751
751







