Доказательство. 1) Пусть существует число l Î R, l ≠ 0 такое, что = l (l ≠ 0)

1) Пусть существует число l Î R, l ≠ 0 такое, что = l (l ≠ 0).

Отложим вектор от точки O’: = .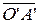

Тогда OO’A’A – параллелограмм (см. § 8), следовательно, O’A’ | | OA.

С другой стороны, точки O’,A’ и B лежат на одной прямой, поэтому OA | | O’B.

2) Пусть векторы 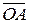= , 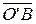= ( ≠ q, ≠ q) и OA | | O’B. Отложим вектор от точки O’: 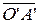= . Тогда четырехугольник OO’A’A является параллелограммом и O’A’ | | OA, значит точки O’,A’ и B лежат на одной прямой.

Та как точки O’ и A’ различны ( ≠ q), то существует такое число l Î R, что точка B делит O’A’ в отношении l. Следовательно, = l .

Определение. Будем называть векторы и коллинеарными, если существует такое число l Î R, что = l или = l .

Обозначение: | | .